Matematik

Hjælp til trekantsberegning

29. september 2020 af 94Amalie - Niveau: C-niveau

Er der nogle, som kan hjælpe mig med at løse denne opgave?

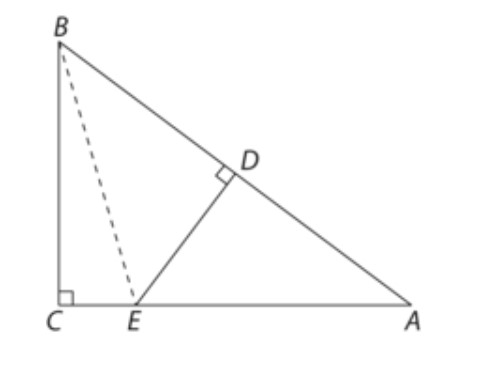
I den retvinklede ABC er AC = 4 og BC = 3. Trekanten foldes om linjen DE, som er vinkelret på hypotenusen i dens midtpunkt D, så B falder sammen med A. Bestem længden af folden DE.

Vedhæftet fil: Skærmbillede 2020-09-29 182815.jpg

Brugbart svar (0)

Svar #1
29. september 2020 af mathon

Brugbart svar (1)

Svar #2
29. september 2020 af mathon

$\small \begin{array}{lllll} \textup{Af ensvinklede}\\ \textup{ trekanter:}\\& \Delta BEC\sim \Delta ABC\\\\& \frac{\left | BE \right |}{\left | AB \right |}=\frac{\left | BC \right |}{\left | AC \right |}=\frac{3}{4}\\\\& \frac{\left | BE \right |}{\left | AB \right |}=\frac{3}{4}\\\\& \left | BE \right |=\frac{3}{4}\cdot \left | AB \right |=\frac{3}{4}\cdot 5=\frac{15}{4}\\ \textup{Pythagoras:}\\& \left | DE \right |=\sqrt{\left | BE \right |^2-\left | BD \right |^2}=\sqrt{\left ( \frac{15}{4} \right )^2-2.5^2} \end{array}$

Svar #3
29. september 2020 af 94Amalie

TUSIND tak for hjælpen! :)

Brugbart svar (1)

Svar #4
29. september 2020 af mathon

$\small \begin{array}{llllll} \textbf{Opgave 8}\\&1.&& \angle A=65\degree\quad \angle B=35\degree\quad c=20\\\\\\&&& \angle C=180\degree-(65\degree+35\degree)=80\degree\\\\&& \textup{sinusrelationerne}\\&& \textup{giver:}\\&& &\frac{a}{\sin(A)}=\frac{c}{\sin(C)}\\\\&&& a=\frac{\sin(A)}{\sin(C)}\cdot c=\frac{\sin(65\degree)}{\sin(80\degree)}\cdot 20\\\\\\&&& \frac{b}{\sin(B)}=\frac{c}{\sin(C)}\\\\&&& b=\frac{\sin(B)}{\sin(C)}\cdot c=\frac{\sin(35\degree)}{\sin(80\degree)}\cdot 20\\\\\\& 2.\\\\&& \textup{Trekantsareal:}&T=\frac{1}{2}\cdot a\cdot c\cdot \sin(B) \end{array}$

Skriv et svar til: Hjælp til trekantsberegning

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.