Matematik

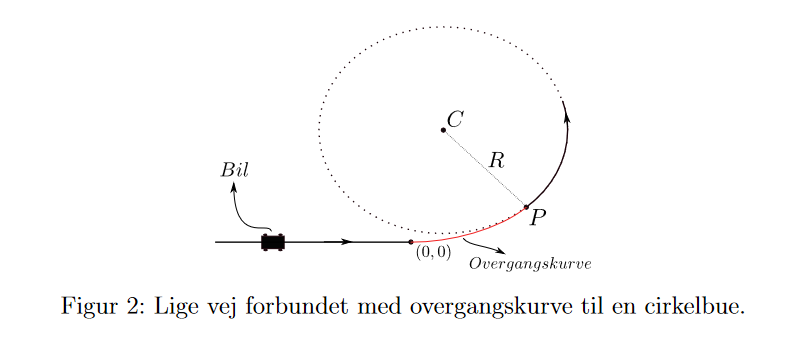
Cirkelbue

09. april 2021 af carlaagaard - Niveau: Universitet/Videregående

Hej Alle,

Jeg har over flere omgange prøvet at vise, at cirkelbuen (nr. 3 vektor i parameterfremstillingen) har en konstant fart = 1. Man skal tage den afledte (hastigheden) og derefter tag længeden (farten), men jeg kan ikke få det til at gå op.

Tak på forhånd :)

Vedhæftet fil: Cirkelbue.png

Brugbart svar (0)

Svar #1
09. april 2021 af mathon

...ingen figur er medsendt.

Svar #2
09. april 2021 af carlaagaard

Det er denne figur...

Vedhæftet fil:Fgur 2.PNG

Brugbart svar (0)

Svar #3
09. april 2021 af mathon

Brugbart svar (0)

Svar #4
09. april 2021 af mathon

Brugbart svar (0)

Svar #5
09. april 2021 af mathon

$\small \begin{array}{llllll} \textbf{(i)}\\&& \textbf{r}(t)=&\begin{pmatrix} t\\0 \end{pmatrix}=\begin{pmatrix} 0\\0 \end{pmatrix}+t\cdot \begin{pmatrix} 1\\0 \end{pmatrix}\quad \textup{er en parameterfremstilling for x-aksen }t\in\mathbb{R}\backslash \mathbb{R}_+\\\\\\&& \textbf{r}(t)=&\begin{pmatrix} x(t)=c_1+R\cdot \cos\left ( \frac{1}{R}\cdot t-\theta \right )\\y(t)= c_2+R\cdot \sin\left ( \frac{1}{R}\cdot t-\theta \right ) \end{pmatrix}\quad t\in\mathbb{R}\backslash\mathbb{R}\\\\&&& \begin{pmatrix} x-c_1=R\cdot \cos\left ( \frac{1}{R}\cdot t-\theta \right )\\ y-c_2=R\cdot \sin\left ( \frac{1}{R}\cdot t-\theta \right ) \end{pmatrix}\\\\&&& (x-c_1)^2+(y-c_2)^2=R^2\cdot \left (\cos^2\left ( \frac{1}{R}\cdot t-\theta \right )+\sin^2\left ( \frac{1}{R}\cdot t-\theta \right ) \right )\\\\&&& (x-c_1)^2+(y-c_2)^2=R^2\quad \textup{hvilket er ligningen for }\\&&&\qquad \qquad \qquad \qquad \qquad \qquad \; \, \textup{cirklen med centrum }C\\&&&\qquad \qquad \qquad \qquad \qquad \qquad \; \, \textup{og radius }R. \end{array}$

Svar #6
09. april 2021 af carlaagaard

Tak for dit svar :)

Men jeg leder faktisk efter at differentiere den tredje vektor (den, der står nederst), og så tag længden af den, således længden (farten) er 1

Vedhæftet fil:ligning for cirkelbue.PNG

Brugbart svar (0)

Svar #7
09. april 2021 af AMelev

$t<0:\: \binom{x}{y}=\binom{t}{0}=\binom{0}{0}+t\cdot \binom{1}{0}$
Det er parameterfremstillingen for en ret linje gennem (0,0) med retningsvektor $\vec r= \binom{1}{0}$ , altså vandret.

$\binom{cos(v)}{sin(v)}$ beskriver enhedscirklen, så $R\cdot \binom{cos(v)}{sin(v)}$ beskriver en cirkel med centrum i (0,0) og radius R.

$C+R\cdot \binom{cos(v)}{sin(v)}$ viser, at cirklen er parallelforskudt i retningen C (som er en vektor, så der burde have stået $\vec c$ i stedet for C).

$\vec r\, '(t)=(\vec c+R\cdot \binom{cos(\frac{t}{R}-\Theta )}{sin(\frac{t}{R}-\Theta )})'= (\binom{c1+R\cdot cos(\frac{t}{R}-\Theta )}{c2+R\cdot sin(\frac{t}{R}-\Theta )})'=$
$\binom{(c1+R\cdot cos(\frac{t}{R}-\Theta ))'}{(c2+R\cdot sin(\frac{t}{R}-\Theta ))'}\overset{*)}{=} \binom{R\cdot \frac{1}{R}\cdot sin(\frac{t}{R}-\Theta )}{R\cdot \frac{1}{R}\cdot cos(\frac{t}{R}-\Theta )} =\binom{sin(\frac{t}{R}-\Theta )}{cos(\frac{t}{R}-\Theta )}$ Enhedscirkel.

*) Se din formelsamling side 24 (135) el. (136) for differentiation af sammensatte funktioner $\frac{t}{R}-\Theta = \frac{1}{R}\cdot t-\Theta$

Brugbart svar (0)

Svar #8
09. april 2021 af mathon

$\small \begin{array}{llllllll}\\& \textup{for }t \geq 1 \\\\&& \textbf{r}{\, }'(t)=\textbf{v}(t)=\begin{pmatrix} -\frac{R}{R}\cdot \sin\left(\frac{1}{R}\cdot t-\theta\right)\\ \frac{R}{R}\cdot \cos\left(\frac{1}{R}\cdot t-\theta\right) \end{pmatrix}=\begin{pmatrix} -\sin\left(\frac{1}{R}\cdot t-\theta\right)\\ \cos\left(\frac{1}{R}\cdot t-\theta\right) \end{pmatrix}\\\\\\&& \left | \textbf{r}{\, }'(t) \right |=\sqrt{\left ( -\sin\left(\frac{1}{R}\cdot t-\theta\right) \right )^2+\left ( \cos\left(\frac{1}{R}\cdot t-\theta\right) \right )^2}\\\\&& \left | \textbf{r}{\, }'(t) \right |=\sqrt{ \sin^2\left(\frac{1}{R}\cdot t-\theta\right) + \cos^2\left(\frac{1}{R}\cdot t-\theta\right) }=1 \end{array}$

Svar #9
09. april 2021 af carlaagaard

Mange tak. Så have jeg faktisk gjort det rigtigt

Svar #10
09. april 2021 af carlaagaard

Hvis jeg så skal finde krumningen på cirkelbuen, således k(t)= 1/R. Hvordan gøres det? På forhånd tak :)

Brugbart svar (0)

Svar #11
09. april 2021 af mathon

$\small \small \begin{array}{llllllll}\\& \textup{for }t \leq 1 \\\\&& \textbf{r}{\, }'(t)=\textbf{v}(t)=\begin{pmatrix} 1\\0 \end{pmatrix}\\\\&& \left | \textbf{r}{\, }' (t)\right |=\sqrt{1^2+0^2}=1 \end{array}$

Brugbart svar (0)

Svar #12
09. april 2021 af mathon

$\begin{array}{llllll}\\& \textup{krumning:}\\&& \kappa =\frac{\dot x\cdot \ddot y-\dot y\cdot \ddot x}{\left | \textbf{v} \right |^3} \end{array}$

Brugbart svar (0)

Svar #13
09. april 2021 af mathon

$\begin{array}{llllll}\\&& \dot x=-\sin\left ( \frac{1}{R}\cdot t-\theta \right )&&&\dot y= \cos\left ( \frac{1}{R} t-\theta \right )\\\\&& \ddot x=-\frac{1}{R}\cos\left ( \frac{1}{R}\cdot t-\theta \right )&&&\ddot y=-\frac{1}{R}\cdot \sin\left ( \frac{1}{R}\cdot t-\theta \right ) \end{array}$

Brugbart svar (0)

Svar #14
10. april 2021 af mathon

$\begin{array}{llllll}\\& \textup{krumning:}\\&& \kappa =\frac{-\sin\left(\frac{1}{R}\cdot t -\theta\right)\cdot \left ( -\frac{1}{R} \right )\cdot \sin\left(\frac{1}{R}\cdot t-\theta \right)-\cos\left ( \frac{1}{R}\cdot t-\theta \right )\cdot \left ( -\frac{1}{R}\right)\cdot \cos\left ( \frac{1}{R}\cdot t-\theta \right ) }{\left | \textbf{v} \right |^3}\\\\&& \kappa =\frac{\frac{1}{R}\cdot \sin^2\left ( \frac{1}{R}\cdot t-\theta \right )+\frac{1}{R}\cdot \cos^2\left ( \frac{1}{R}\cdot t-\theta \right )}{1^3} \\\\&& \kappa =\frac{1}{R}\cdot\left ( \cos^2\left (\frac{1}{R}\cdot t-\theta \right )+ \sin^2\left (\frac{1}{R}\cdot t-\theta \right ) \right )\\\\&& \kappa =\frac{1}{R} \end{array}$

Skriv et svar til: Cirkelbue

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.