Matematik

finde vinkel i kegle

27. april 2021 af aniqu - Niveau: B-niveau

Hej

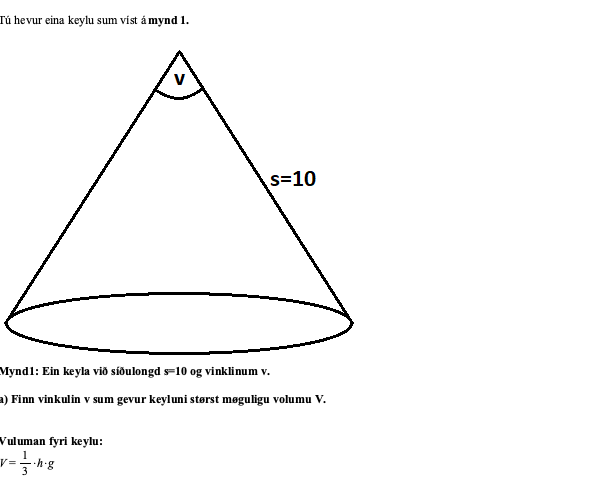
min opgave er at finde en vinkel i en kegle

MEN, det eneste jeg kender er siden som er 10.

Vedhæftet fil: Skærmbillede 2021-04-27 kl. 15.53.02.png

Brugbart svar (0)

Svar #1
27. april 2021 af peter lind

Brugbart svar (2)

Svar #2
27. april 2021 af peter lind

Jeg kan ikke forstå det sprog der bruges i figuren og der er ikke nok informationer til at jeg kan klare den. Vil du ikke oversætte det ?

Brugbart svar (0)

Svar #3
27. april 2021 af AMelev

#0 Du skal ikke finde vinklen som sådan, men finde den vinkel, der giver det største rumfang.

Så skal du bestemme V(v) = f(v) = 1/3·g·h, da det er lidt forvirrende at have afhængig variabel til at hedde V og uafhængig variabel til at hedde v.
Derefter skal du finde max f(v) på sædvanlig vis ved af løse f '(v) = 0 og derudfra bestemme max.
Vær obs på, om du opererer i rad eller i grader.

Vedhæftet fil:Udklip.JPG

Svar #4
28. april 2021 af aniqu

Okey tak. Skal man så sætte g og h ind for formelen, og så sætte f’(x)=0 ind for f(x)?

Brugbart svar (0)

Svar #5
28. april 2021 af AMelev

Der står jo faktisk ikke, at du skal bestemme max volumen, men du må selvfølgelig gerne gøre det.

Svar #6
28. april 2021 af aniqu

Faktiskt står der en texst ovenfor at det skal være max volumen, jeg glemte føre det ind med

Brugbart svar (0)

Svar #7
03. maj 2021 af mathilde098765432

#3 isolerer du h og g som ukendte ligninger først, og hvordan finder du frem til funktionen f(v)? Tak

Brugbart svar (0)

Svar #8
03. maj 2021 af mathilde098765432

Finder du vinkelen som var det en retvinklet trekant, så til sidst ganger med 2 for at finde den fulde vinkel?

Brugbart svar (0)

Svar #9
03. maj 2021 af ringstedLC

#7:

$\begin{align*} \cos\left ( \tfrac{v}{2} \right )=\frac{h}{s}\Rightarrow h&=s\cdot \cos\left ( \tfrac{v}{2} \right ) \\ h&=10\cdot \cos\left ( \tfrac{v}{2} \right ) \\ g&=10\cdot \sin\left ( \tfrac{v}{2} \right ) \\ R &= \tfrac{1}{3}\cdot hg \\ R(v)&= \tfrac{10^2}{3}\cdot \cos\left ( \tfrac{v}{2} \right )\cdot \sin\left ( \tfrac{v}{2} \right ) \\ \end{align*}$

Brugbart svar (0)

Svar #10
03. maj 2021 af ringstedLC

Alternativ til optimering/differentiering: Se på forskriften for R(v):

$\begin{align*} R_{maks}(v)=\Bigl(\cos\left (\tfrac{v}{2}\right )\cdot \sin\left ( \tfrac{v}{2} \right )\Bigr)_{maks} \Rightarrow \cos\left (\tfrac{v}{2}\right ) &= \sin\left ( \tfrac{v}{2} \right )\\ \tfrac{v}{2} &=\;?\Rightarrow v=\;? \end{align*}$

Alternativ 2:

Keglens tværsnit er en ligebenet trekant. Tænk over hvilken kombination af vinkler, der gør dens A = 1/2 h grundlinje størst. Og brug så, at størst tværsnit ⇒ størst rumfang.

Brugbart svar (0)

Svar #11
03. maj 2021 af AMelev

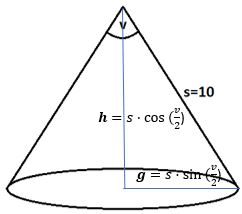
#8 Højden går fra keglens spids vinkelret på grundfladen og danner dermed sammen med grundfladens radius r en retvinklet trekant, hvor vinklen i toppen af trekanten er halvdelen af keglens topvinkel v.
Der er en skrivefejl. Der skulle have stået r = ... i stedet for g =..., så jeg forstår godt, du undres.
g er jo grundfladesn areal, så $g=\pi\cdot r^2=\pi\cdot (10\cdot sin(\frac{v}{2}))^2$ og
$h= 10\cdot cos(\frac{v}{2})$
Dermed bliver rumfanget af keglen
$f(v)=\frac{1}{3}\cdot 10\cdot cos(\frac{v}{2})\cdot \pi\cdot (10\cdot sin(\frac{v}{2}))^2= \frac{1000\pi}{3}\cdot cos(\frac{v}{2})\cdot (sin(\frac{v}{2}))^2$ , hvor 0 < v < 180º

NB! Notationsfejlen føres videre i #9 og #10, så de dur desværre ikke direkte. Undskyld ringstedLC m.fl.

Vedhæftet fil:Udklip-1.JPG

Brugbart svar (0)

Svar #12
03. maj 2021 af ringstedLC

Ingen årsag, - den burde jeg selv have spottet.

Skriv et svar til: finde vinkel i kegle

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.