Matematik

Linjens en ligning for linjen l

06. maj 2021 af UCL (Slettet) - Niveau: B-niveau

Jeg har svært ved at få startet det her spørgsmål, hvordan starter jeg på det

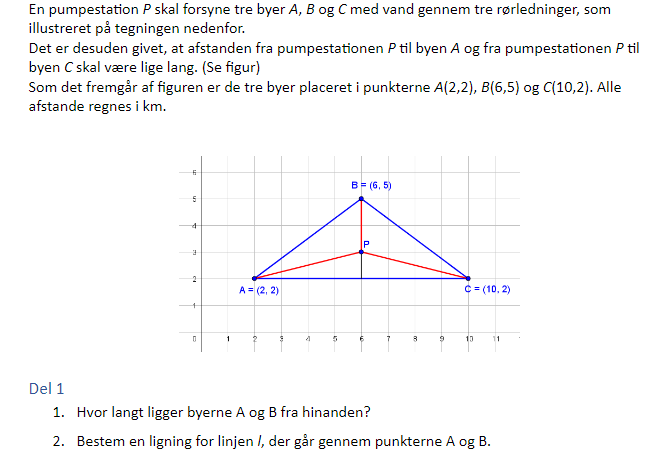
Bestem en ligning for linjen l, der går gennem punkterne A og B.

Vedhæftet fil: Ligning for linjen l VS.png

Brugbart svar (1)

Svar #1
06. maj 2021 af PeterValberg

Jeg indsætter lige dit vedhæftede billede, det gør det lidt nemmere at hjælpe

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (0)

Svar #2
06. maj 2021 af mathon

Find en normalvektor til linjen.

Svar #3
06. maj 2021 af UCL (Slettet)

Okay. Kan man slet ikke lave opgaven uden vektorregning ? Jeg mener altså virkelig ikke jeg har lært om det

Brugbart svar (0)

Svar #4
06. maj 2021 af PeterValberg

Bestem en ligning for linjen l, der går gennem punkterne A og B.

Du kan gøre det på samme måde, som når du skal bestemme en forskrift
for en lineær funktion gennem to kendte punkter, i stedet for f(x) skriver du bare y

eller du kan gøre som i video nr. 21 på denne videoliste < LINK >
benyt fx punkt A som det kendte punkt og tværvektoren til vektor AB som normalvektor

- - -

mvh.

Peter Valberg
(YouTube)

Svar #5
06. maj 2021 af UCL (Slettet)

Jeg har set videon nu, tak for det. Det hjælper en lille smule, men jeg er stadig i tvivl om hvordan jeg skal starte med mine punkter fra opgaven.

Brugbart svar (0)

Svar #6
06. maj 2021 af mathon

$\small \small \begin{array}{llllll} \textbf{2.}\\& \textup{en retningsvektor er:}\\&& \overrightarrow{r}=\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}=\begin{pmatrix} 6\\5 \end{pmatrix}-\begin{pmatrix} 2\\2 \end{pmatrix}=\begin{pmatrix} 4\\ 3 \end{pmatrix}\\\\& \textup{en normalvektor er:}\\&& \overrightarrow{n}=-\widehat{\overrightarrow{r}}=-\begin{pmatrix} -3\\4 \end{pmatrix}=\begin{pmatrix} 3\\-4 \end{pmatrix} \\\\\\& \textup{N\aa r }P(x,y)\textup{ er et}&\textup{vilk\aa rligt punkt p\aa \ }l\\&\textup{g\ae lder:}\\&& l\textup{:}\quad \overrightarrow{n }\cdot\overrightarrow{AP}=0\\\\&& l\textup{:}\quad \overrightarrow{n}\cdot\left ( \overrightarrow{OP}-\overrightarrow{OA} \right )=0\\\\&& l\textup{:}\quad \begin{pmatrix} 3\\-4 \end{pmatrix}\cdot \begin{pmatrix} x-2\\y-2 \end{pmatrix}=0\\\\&& l\textup{:}\quad 3x-6-4y+8=0\\\\\\&& l\textup{:}\quad 3x-4y+2=0\\\\&& l\textup{:}\quad y=\frac{3}{4}x+\frac{1}{2} \end{array}$

Brugbart svar (1)

Svar #7
06. maj 2021 af AMelev

Du kan gøre, som du gjorde i folkeskolen. Se din formelsamling side 13 (62)-(64)
Kald det ene punkt (x1,y1) og det andet (x2,y2).
Indsæt i formlen for a og bestem derefter b.

Alternativt kan du bruge dit grafværktøj, hvis hjælpemidler er tilladt.
Afsæt punkterne, tegn linjen gennem dem og få ligningen.

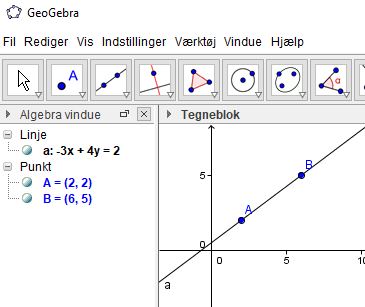
Hvilket CAS-værktøj bruger du?

Vedhæftet fil:Udklip-2.jpg

Svar #8
06. maj 2021 af UCL (Slettet)

Ja, altså det virker lidt lettere, jeg vil prøve at skrive det hele ned, så kan jeg vise det til min lærer og se om vi må lave det på den måde, ellers kommer han måske til at forklarer mig hvad jeg ellers skal gøre. 1000 tak. Jeg bruger wordmat til ligninger og funktioner og også geogebra. 1000 tak

Brugbart svar (0)

Svar #9
06. maj 2021 af PeterValberg

GeoGebra har en særlig kommando:

Linje(<punkt>,<punkt>)

som du kan bruge

Linje((2,2),(6,5))

så kommer det helt af sig selv :-)

- - -

mvh.

Peter Valberg
(YouTube)

Skriv et svar til: Linjens en ligning for linjen l

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.