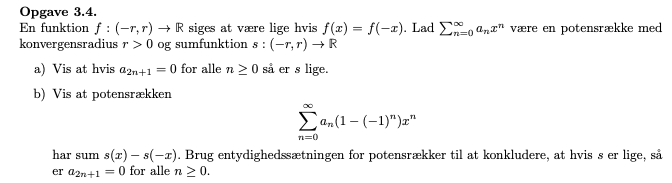Matematik

Sumfunktion

05. juni 2021 af K22 - Niveau: Universitet/Videregående

Hej. Kan I give nogle hints til a) og b)?

Vedhæftet fil: Skærmbillede 2021-06-05 kl. 22.54.01.png

Brugbart svar (1)

Svar #1
06. juni 2021 af AskTheAfghan

(a) Hint: s(-x) = Σ_n≥0 a_n(-x)ⁿ = Σ_n≥0 (a_2n+1(-x)²ⁿ⁺¹+a_2n(-x)²ⁿ) = .. *udfyld her* .. = s(x)

(b) Hint: Del rækken op i to rækker, og vis at summen er s(x) - s(-x). Hvad siger entydighedssætningen? (Hvilken bog er skal der bruges?)

Svar #2
06. juni 2021 af K22

#1 Mange tak :) Bogen der skal bruges er Analyse 1, 3 udgave af Mathias Christiandl.

Svar #3
06. juni 2021 af K22

Skal n ikke være større end eller lig 1? Og summer vi ikke op til uendelig?

Svar #4
06. juni 2021 af K22

Beklager der står jo, at n >= 0 :-)

Brugbart svar (0)

Svar #5
06. juni 2021 af Soeffi

#0.

Brugbart svar (0)

Svar #6
06. juni 2021 af AskTheAfghan

(b) Hint: Hvis s er lige, så er Σ_n≥0 a_n(1-(-1)ⁿ)xⁿ = s(x) - s(-x) = 0 = Σ_n≥0 0xⁿ. Prøv at tage den herfra vha. Sætning 4.35.

Brugbart svar (0)

Svar #7
10. juni 2021 af Ledaniel

Jeg kunne rigtig godt bruge noget hjælp til a).

Kan det passe at $a_{2n+1}(-x)^{2n+1}$ forsvinder i hintet i #1 siden $a_{2n+1}=0$ , og at der tilbage står $\sum_{n=0}^{\infty}a_{2n}(-x)^{2n}$ , som jo er lige for alle n større end nul.

Hvad gør man herfra?

Brugbart svar (0)

Svar #8
10. juni 2021 af Soeffi

#7. Når a_2n+1 = 0, så får du:
$\sum_{n=0}^{\infty}a_{2n}\cdot x^{2n}$
Denne sumfunktion er lige, fordi den er en sum af lige funktioner: x², x⁴, x⁶,...

$\sum_{n=0}^{\infty}a_{n}\cdot(1-(-1)^n)\cdot x^{n}=\sum_{n=0}^{\infty}a_{n} \cdot x^{n}-a_{n} \cdot (-1)^n\cdot x^{n}=$

$\sum_{n=0}^{\infty}a_{n} \cdot x^{n}-\sum_{n=0}^{\infty}a_{n} \cdot (-x)^{n}=s(x)-s(-x)$

Skriv et svar til: Sumfunktion

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.