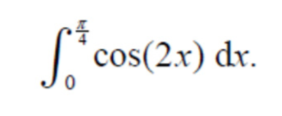Matematik

Integralregning - HASTER!!

20. september 2021 af STE02 - Niveau: A-niveau

Hej,

Jeg skal bestemme integralet, som er vedhæftet. Jeg er ikke sikker på, hvordan det bestemmes, da det er uden hjælpemidler - er der nogen derude, der kan forklare mig, hvordan man kommer frem til svaret

Tak på forhånd!

Vedhæftet fil: Skærmbillede 2021-09-20 kl. 11.35.39.png

Brugbart svar (0)

Svar #1
20. september 2021 af mathon

Brugbart svar (0)

Svar #2
20. september 2021 af Eksperimentalfysikeren

Yndfør en ny variabel, u =2x. du får så, at dx = du/2. Den halve sætter du udenfor integraltegnet. Husk, at grænserne nu skal være u-værdier, så du skal regne dem om. Herfra skulle det være simpelt.

Svar #3
20. september 2021 af STE02

Altså det er uden hjælpemidler - er der ingen metode, der er mere 'simpel'? har ikke hørt om at indføre en ny variabel i undervisningen

Brugbart svar (0)

Svar #4
20. september 2021 af mathon

$\begin{array}{llllll}\textup{s\ae t}&&u=2x&\textup{og dermed }\frac{1}{2}\mathrm{d}u=\mathrm{d}x\qquad \int_{0}^{\frac{\pi}{4}}\rightarrow \int_{0}^{\frac{\pi}{2}}\\\\\\ \textup{substitution:}&&\int_{0}^{\frac{\pi}{4}}\cos(2x)\mathrm{d}x=&\frac{1}{2}\cdot \int_{0}^{\frac{\pi}{2}}\cos(u)\mathrm{d}u=\frac{1}{2}\cdot \left [\sin(u) \right ]_{0}^{\frac{\pi}{2}}=\\\\&&& \frac{1}{2}\cdot \left (\sin\left ( \frac{\pi}{2} \right )-\sin\left ( 0 \right ) \right )=\frac{1}{2}\cdot 1=\frac{1}{2} \end{array}$

Brugbart svar (0)

Svar #5
20. september 2021 af mathon

Hvis du ikke i undervisningen er blevet præsenteret for indførelse af "en ny variabel",
må du klare integrationen pr. snarrådighed:

$\small \begin{array}{llllll} \textup{Da }&&\left (\sin(2x) \right ){}'=\cos\left ( 2x \right )\cdot 2=2\cos(2x)\\\\ \textup{er}&&\left (\frac{1}{2}\sin(2x) \right ){}'=\frac{1}{2}\cdot \cos\left ( 2x \right )\cdot 2=\cos(2x)\\\\ \textup{dvs}&&\textup{en stamfunktion til }\cos(2x)\textup{ er }\frac{1}{2}\sin(2x) \\\\\\&& \int_{0}^{\frac{\pi}{4}}\cos(2x)\mathrm{d}x=\left [ \frac{1}{2}\cdot \sin(2x) \right ]_{0}^{\frac{\pi}{4}}=\frac{1}{2}\cdot \sin\left (2\cdot \frac{\pi}{4} \right )-\frac{1}{2}\cdot \sin\left (2\cdot 0 \right )=\frac{1}{2}\cdot 1=\frac{1}{2} \end{array}$

Skriv et svar til: Integralregning - HASTER!!

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.