Matematik

Differentering vha. produktregel

12. januar 2022 af Guleroden1 - Niveau: B-niveau

Hej, jeg kan simpelthen ikke komme videre i den her opgave,

hvordan reducerer det mest muligt før jeg sætter f'(1)?

Vedhæftet fil: Skærmbillede 2022-01-12 kl. 20.36.37.png

Svar #1
12. januar 2022 af Guleroden1

Jeg benytter produktreglen men kan ikke finde ud af at addere de to led sammen

Svar #2
12. januar 2022 af Guleroden1

Hvordan løser jeg det her i hånden?

Vedhæftet fil:Skærmbillede 2022-01-12 kl. 20.59.08.png

Brugbart svar (0)

Svar #3
12. januar 2022 af StoreNord

#0
Kvadratrod x er x^½. Det skal du bare gange ind i parentesen.

Brugbart svar (0)

Svar #4
12. januar 2022 af StoreNord

#2
Kvadratrod x er x^½. Det kan du forkorte brøken med.
Forkort også med 2.

Brugbart svar (0)

Svar #5
12. januar 2022 af ringstedLC

Brugbart svar (1)

Svar #6
12. januar 2022 af ringstedLC

#2: Det behøver du heller ikke:

$\begin{align*} f'(x) &= \frac{1}{2\sqrt{x}}\cdot (x^3+9)+\sqrt{x}\cdot 3x^2 \\ &= \frac{x^3+9}{2\sqrt{x}}+3x^{2.5} \\ f'(1) &= \frac{1^3+9}{2\sqrt{1}}+3\cdot 1^{2.5}= \end{align*}$

Svar #7
12. januar 2022 af Guleroden1

#6
#2: Det behøver du heller ikke:

$\begin{align*} f'(x) &= \frac{1}{2\sqrt{x}}\cdot (x^3+9)+\sqrt{x}\cdot 3x^2 \\ &= \frac{x^3+9}{2\sqrt{x}}+3x^{2.5} \\ f'(1) &= \frac{1^3+9}{2\sqrt{1}}+3\cdot 1^{2.5}= \end{align*}$

Når ja for pokker! Jeg prøver også det der men jeg fik 13/2? men det er fordi jeg lige brugte regneartets hierarki forkert, men mange tak! endelig

Svar #8
12. januar 2022 af Guleroden1

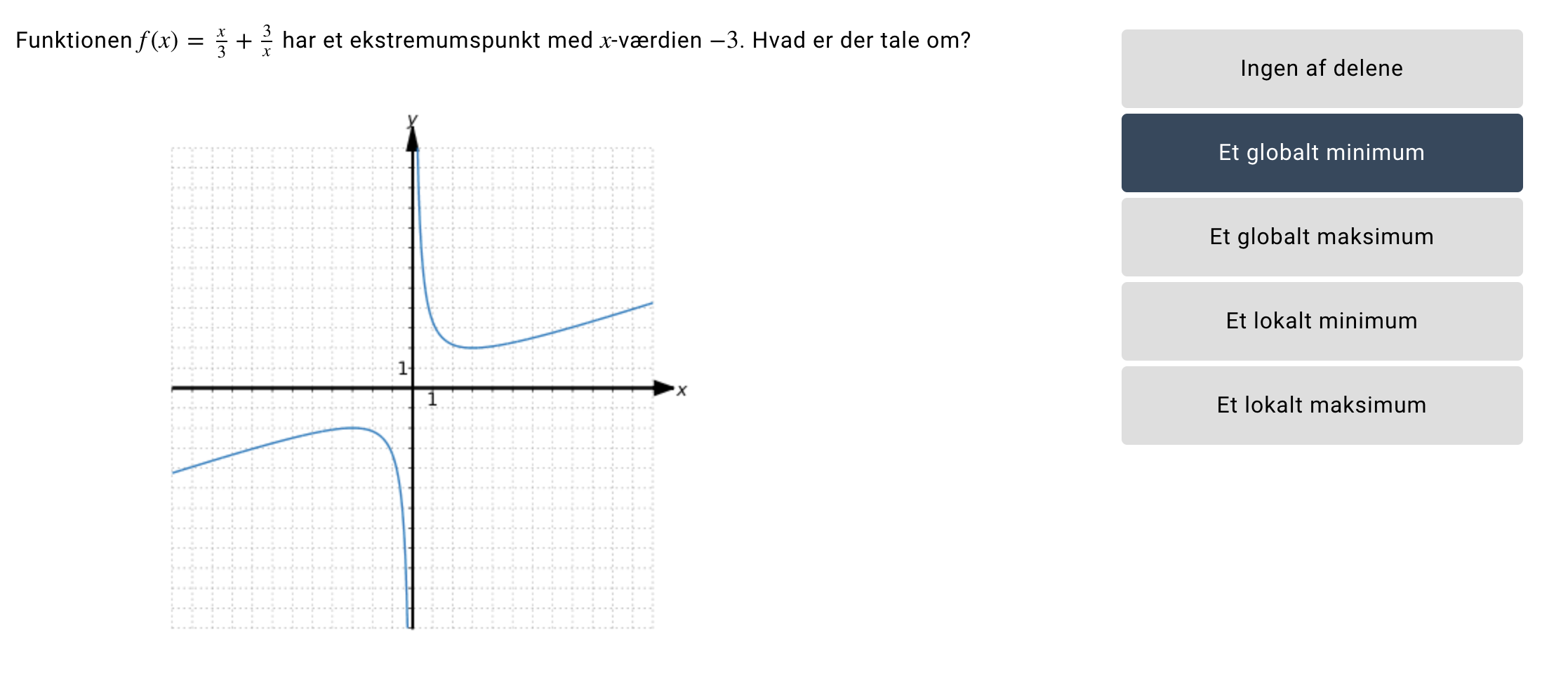
Nu da jeg lige har jer her, er dette her ikke et globalt minimum da grafen er lukket eller sammenhængende?

Vedhæftet fil:Skærmbillede 2022-01-12 kl. 21.43.51.png

Brugbart svar (0)

Svar #9
12. januar 2022 af ringstedLC

Brugbart svar (0)

Svar #10
12. januar 2022 af ringstedLC

#8: Det er da ihvertfald ikke et minimum.

Svar #11
12. januar 2022 af Guleroden1

#10
#8: Det er da ihvertfald ikke et minimum.

Hvordan er det et maksimum så?

Brugbart svar (0)

Svar #12
12. januar 2022 af StoreNord

Det er et lokalt maksimum.

Skriv et svar til: Differentering vha. produktregel

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.