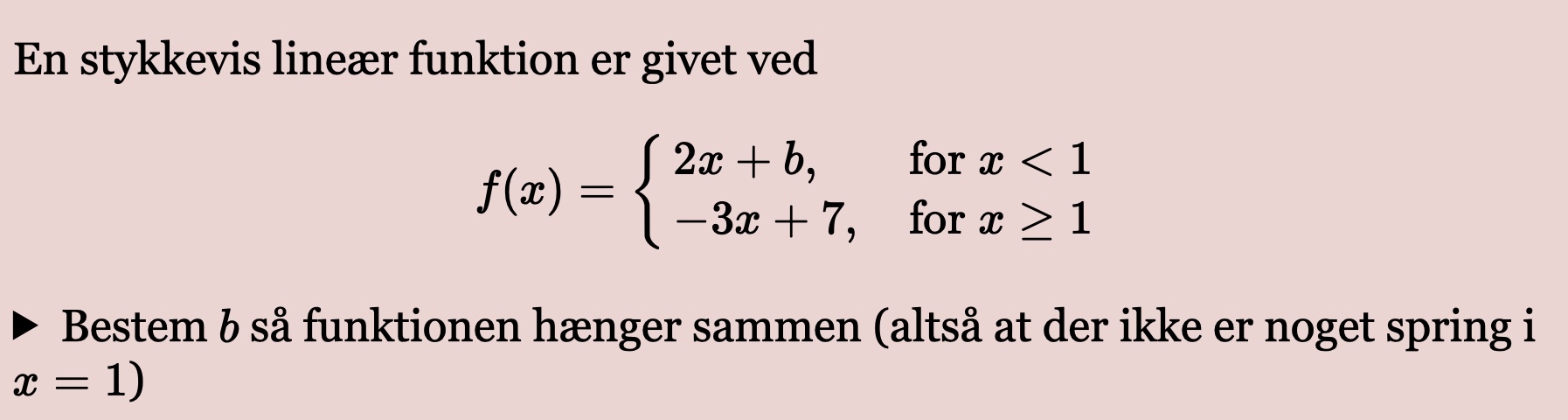Hvad er gaffelforskrifter? Hvordan bruger/regner man dette ud?

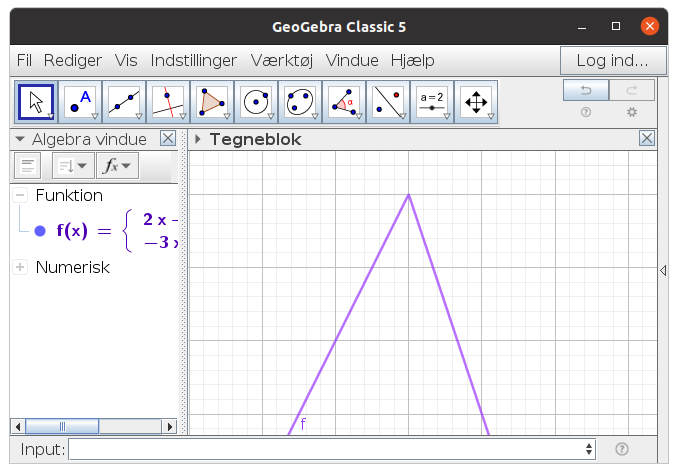
En gaffelforskrift ser du på billedet, altså f(x).
Kald de 2 delfunktioner g(x) og h(x).

Find h(1).

g(1) skulle gerne have den samme y-værdi i x=1.
Løs ligningen:   g(1) = h(1)

Tegn derefter f(x) på kvadreret papir eller med Geogebra.

"Gaflen" ses ved at "f(x)" deles i to eller flere grene på gaflen. Gaffelfunktioners delforskrifter er forsynet med kriterier, der afgør hvilken gren, der skal bruges til hvilken x-værdi.

#4

"Gaflen" ses ved at "f(x)" deles i to eller flere grene på gaflen. Gaffelfunktioners delforskrifter er forsynet med kriterier, der afgør hvilken gren, der skal bruges til hvilken x-værdi.

Fistår intet med ''grene''. Det giver slet ingen mening.

Hvad er de der hajmunder for? Hvad har det af betydning?

Kunne det ikke ligeså godt være:

''Regn disse to formler ud: f(x)=3x+6      & g(x)=4x+6''

Og så går beregningen således i et matematikprogram/app:

solve(0.7*x + 5 = 10*10.8^x)

?

Det blev så nærmest en stegegaffel med to "grene".

# 7
Den kan måske give os kammertonen på 440 svingninger pr. sek?

Når du har fundet b, kan du starte Geogebra og skrive:         Hvis(x < 1, 2x + b, -3 x + 7)

En hajmund kaldes også en Tuborg-hat.

#8 Stegegaffel, ikke stemmegaffel, men hvem ved?

Beklager de manglende evner i frihåndstegning!

Jeg fejllæste instrumentet som en stemmegaffel og så ikke først teksten.
En stemmegaffel vil også være adskilt med grenene og grebet således, at ens hånd ikke svinger med.
# 10 En hyggelig bil - fra før verden gik af lave.

Med "hajmund" mener du vel "<" eller ">". "<" betyder "mindre end", f.eks. "2<5" betyder "2 er mindre end 5". Tilsvarende betder ">" "større end". "≥" betyder større end eller lig med". "2<5" kaldes et udsagn. Et udsagn kan være sandt eller falsk. Dette udsagn er sandt, mens "2>5" er et falskt udsagn. "x<1" kaldes et åbent udsagn fordi man ikke kan afgøre, om det er sandt eller falsk før man ved, hvad x er.

Gaffelfunktionen har to (eller flere) forskrifter hver efterfulgt af et åbent udsagn. Når man skal finde funktionsværdien for en bestemt x-værdi, finder man den gren, hvor det åbne udsagn bliver et sandt udsagn, når man indsætter x-værdien i stedet for x, og benytter så den forskrift, der står i samme linie.

Om Tuborgvognen: Det ejendommelige tag over førerhuset er en efterligning af en paraply, der var anbragt over kuskesædet på Tuborgs hestevogne. Det er tegnet "{", der kaldes en Tuborgparentes, fordi det ligner paraplyen.

#14:

#13

"x<1" kaldes et åbent udsagn fordi man ikke kan afgøre, om det er sandt eller falsk før man ved, hvad x er.

Og da x er den uafhængige variabel, er det optil "brugeren" af forskriften, at sørge for, at udsagnet bliver sandt inden han indsætter x i forskriften og beregner funktionsværdien.

Bemærk: De to udsagn for opgavens forskrift gør det muligt at gøre netop en af delforskrifterne sande uanset hvilken x-værdi, der vælges.

#16 Jeg ville følge anvisningen i #1.

1) Der står, "Kald de 2 delfunktioner g(x) og h(x)". Fint, lad g(x) = 2x + b og h(x) = -3x +7;                            2) Dernæst står der "Find h(1)". I funktionen h skal du erstatte bogstavet x med tallet 1, og                                 regne dvs. h(1) = -3·1 + 7 = ...                                                                                                                          3) I #1 skrives, at "g(1) skulle gerne have den samme y-værdi i x=1" Med y-værdi menes                                 det tal du ville få af regnestykket -3·1 + 7. Dernæst er g(1) = 2·1 + b = 2 + b. Altså betyder skrivelsen at 2 +      b skal være lig med tallet. Du får en ligning, talværdien for b ikke kendes. Ka' du løse ligningen?                  4)  "Løs ligningen:   g(1) = h(1). Tegn derefter f(x) på kvadreret papir eller med Geogebra" Dette trin er        for at tjekke, grafisk og ved udregninger, om du har fået den rette tal-værdi for b. 

.

Jeg vil sige, med krav om kontinuitet for x = 1 må gælde:
f (x) → 2 + b  for x → 1_-     ∧      f (x) → 4 for x → 1₊       ⇒       2 + b = 4
(De små indeks fortegn betyder x gående fra venstre henh.vis. fra højre). 
 

#18 Kontinuitetskravet er langt over trådskriverens faglige niveau. 

#17

#16 Jeg ville følge anvisningen i #1.

1) Der står, "Kald de 2 delfunktioner g(x) og h(x)". Fint, lad g(x) = 2x + b og h(x) = -3x +7;                            2) Dernæst står der "Find h(1)". I funktionen h skal du erstatte bogstavet x med tallet 1, og                                 regne dvs. h(1) = -3·1 + 7 = ...                                                                                                                          3) I #1 skrives, at "g(1) skulle gerne have den samme y-værdi i x=1" Med y-værdi menes                                 det tal du ville få af regnestykket -3·1 + 7. Dernæst er g(1) = 2·1 + b = 2 + b. Altså betyder skrivelsen at 2 +      b skal være lig med tallet. Du får en ligning, talværdien for b ikke kendes. Ka' du løse ligningen?                  4)  "Løs ligningen:   g(1) = h(1). Tegn derefter f(x) på kvadreret papir eller med Geogebra" Dette trin er        for at tjekke, grafisk og ved udregninger, om du har fået den rette tal-værdi for b. 

.

jeg forstår det indtil trin 2 og er faldet fra ved trin 3, da jeg ikke forstår hvad b er/hvordan det skal brues/hvor det kommer fra?