Matematik

Marathon banen

03. februar kl. 02:50 af SuneChr - Niveau: A-niveau

. SP 030220230250.PNG

Vedhæftet fil: SP 030220230250.PNG

Brugbart svar (0)

Svar #1
03. februar kl. 22:07 af jl9

Jeg undlader at tage løbeturen og kommer med et bud i stedet:

$r=b=\frac{42.195}{\left ( \pi+2 \varphi \right ) \int_{0}^{ \pi / 2} \sqrt{1-(1/\varphi) \sin^2 \left ( \theta \right ) } \mathrm{d} \theta }$

Brugbart svar (0)

Svar #2
03. februar kl. 22:33 af jl9

$r=b=\frac{42.195}{\left ( \pi+2 \varphi \int_{0}^{ \pi / 2} \sqrt{1-(1/\varphi) \sin^2 \left ( \theta \right ) } \mathrm{d} \theta \right ) }$

Svar #3
04. februar kl. 02:08 af SuneChr

Fuldstændig enig med # 2.
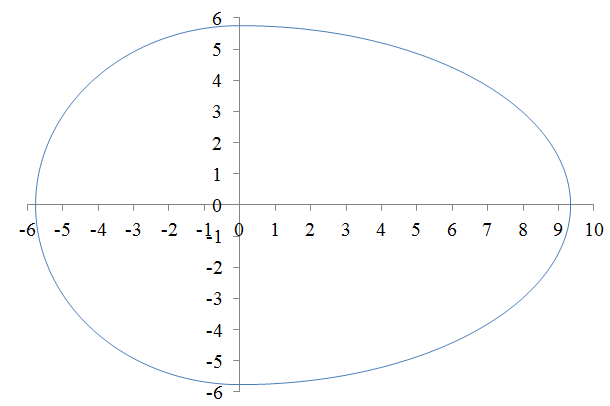
Ellipsens excentricitet = $\sqrt{\frac{\sqrt{5}-1}{2}}$
Med tre rigtige decimaler: a = 9,337... b = r = 5,771...
Man må hermed sige, at banen er kridtet op ned til den enkelte meter.

Svar #4
05. februar kl. 01:35 af SuneChr

. SP 050220230136.PNG

Vedhæftet fil:SP 050220230136.PNG

Brugbart svar (0)

Svar #5
05. februar kl. 22:06 af jl9

Smukt. Den bliver svær at finde plads til.

Brugbart svar (0)

Svar #6
05. februar kl. 22:11 af jl9

Jeg håber ikke der kommer landskabs højdeforskelle med i den næste opgave!

Svar #7
06. februar kl. 20:55 af SuneChr

# 5 og 6
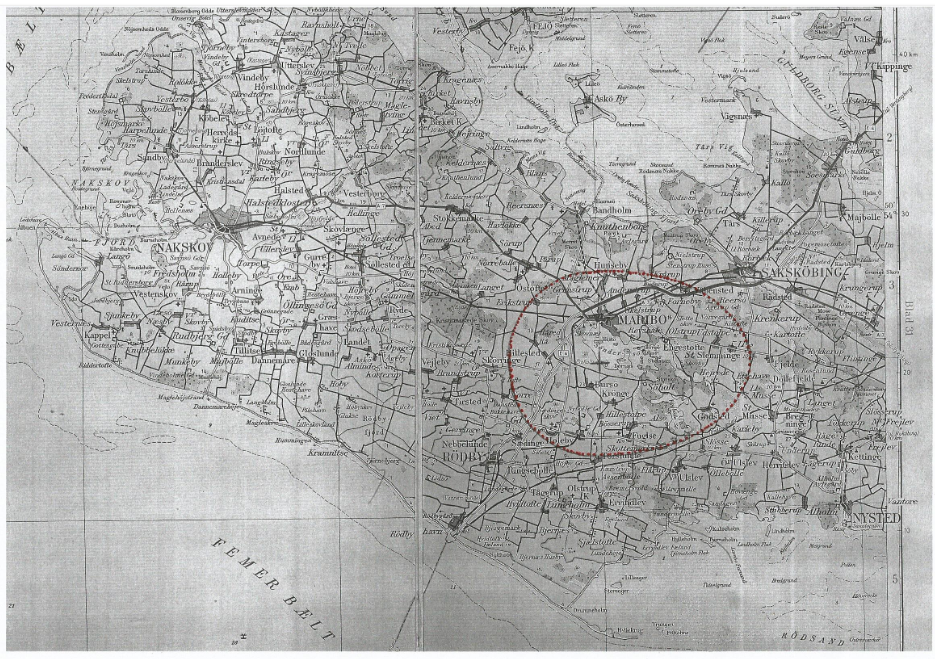
Banen anlægges, på det flade Lolland,
med det fælles centrum for cirklen og ellipsen i punktet 54º45' n.b. 11º30' ø.l.
som er sammenfaldende med ellipsens lilleakse.

Banen skal også anvendes til en halv-Marathon, hvorfor MÅL hertil markeres på banen.
START til såvel hel- som halv-Marathon anlægges i punktet (0 , b) # 4 , Hunseby Fig. 2
og løbsretningen i positiv omløbsretning.

Hvor stor en vinkel gennemløber radiusvektor fra START til MÅL ved en halv-Marathon?

Fig. 1

Fig. 2

Vedhæftet fil:Marathon Lolland Fig. 2.PNG

Svar #8
06. februar kl. 20:59 af SuneChr

. Marathon Lolland Fig. 1.PNG

Vedhæftet fil:Marathon Lolland Fig. 1.PNG

Brugbart svar (0)

Svar #9
07. februar kl. 17:37 af jl9

Det skal nok blive modtaget med stor velvilje blandt lokalbefolkningen. Mit bud er vinklen V som opfylder nedenstående. Men jeg har ikke været i stand til at løse eller approksimere udtrykket.

$\frac{42.195}{2} = b\pi + \int _{\pi}^{V}\sqrt{\varphi^2 b^2 \sin^2(\theta) + b^2\cos^2(\theta)} \mathrm{d} \theta$

Svar #10
09. februar kl. 04:47 af SuneChr

# 9
Helt enig, - omend jeg har benyttet et andet integral

$a\cdot \int_{0}^{0,3211}\sqrt{1-k^{2}\sin ^{2}\Theta }\, \textup{d}\Theta$ hvor øvre grænse er ca. 18,4º og excentriciteten = k
Vinklen er da i alt ca. 198,4º

Brugbart svar (0)

Svar #11
09. februar kl. 23:40 af jl9

Dvs. let sydøst for Fuglse kro. Udmærket sted :-)

Skriv et svar til: Marathon banen

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.