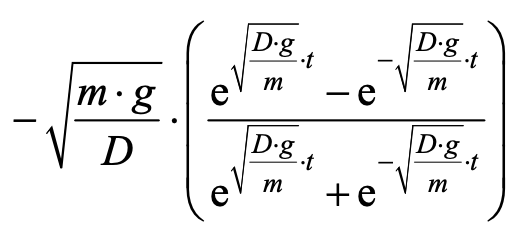Studieretningsprojekt/-opgave (SRP/SRO)

Udledning af dette udtryk

17. marts kl. 23:12 af Rebecca1234a

Hej alle,

Jeg er lige pt i gang med at skrive SRP i mat og fysik, og jeg i min opgaveformulering er jeg blevet beedt om at udlede dette udtryk som er vedhæftet nedenunder. Jeg har nu siddet med det i et stykke tid, og jeg ved ikke helt hvad jeg skal gøre.

Og det skal lige siges at man skal inddrage teknikken af separation af variable, når man udleder den.

Er der en venlig sjæl der kan hjælpe mig, for den stresser mig en hel del! :)))

Vedhæftet fil: Skærmbillede 2023-03-17 kl. 23.11.43.png

Brugbart svar (0)

Svar #1
17. marts kl. 23:16 af peter lind

Brugbart svar (1)

Svar #2
17. marts kl. 23:21 af peter lind

tror du vi kan udlede et udtryk uden at vi ved noget som helst om udtrykket ? Kom dog med en ordentlig forklaring!

Brugbart svar (0)

Svar #3
18. marts kl. 08:30 af BirgerBrosa

Det ligner et udtryk der har noget med frit fald at gøre.

Kald $z = \sqrt{\frac{Dg}{m}}$ så kan udtrykket reduceres til

$-\sqrt{\frac{mg}{D}} \cdot \tanh(zt)$

Svar #4
18. marts kl. 11:14 af Rebecca1234a

Okay undskyld! men her er forklaringerne.

Vedhæftet fil:Skærmbillede 2023-03-18 kl. 11.13.30.png

Svar #5
18. marts kl. 11:14 af Rebecca1234a

del 2 er her

Vedhæftet fil:Skærmbillede 2023-03-18 kl. 11.13.57.png

Svar #6
18. marts kl. 11:15 af Rebecca1234a

#3
Det ligner et udtryk der har noget med frit fald at gøre.

Kald $z = \sqrt{\frac{Dg}{m}}$ så kan udtrykket reduceres til

$-\sqrt{\frac{mg}{D}} \cdot \tanh(zt)$

Og ja det er med lodret fald med luftmodstand:))

Brugbart svar (0)

Svar #7
18. marts kl. 11:53 af jl9

Hvor langt er du kommet?

Brugbart svar (0)

Svar #8
18. marts kl. 12:17 af jl9

$\\ m \cdot v' = -m \cdot g + D \cdot v^2 \\ v' = \frac{1}{m} \left( -m \cdot g + D \cdot v^2 \right ) \\ v' = \frac{D}{m} \left( -m \cdot g / D + v^2 \right ) \\ v' = \frac{D}{m} \left( v^2 - \sqrt{m \cdot g / D }^2\right )$

$\\ v'=\frac{D}{m}\cdot\left(v^2 - k^2 \right ) \\ \frac{dv}{dt}=\frac{D}{m}\cdot\left(v^2 - k^2 \right ) \\ \frac{dv}{dt}\frac{1}{v^2 - k^2 }=\frac{D}{m} \\ \int \frac{dv}{dt}\frac{1}{v^2 - k^2 } dt= \int \frac{D}{m} dt$

Svar #9
18. marts kl. 12:48 af Rebecca1234a

#8
b)

$\\ m \cdot v' = -m \cdot g + D \cdot v^2 \\ v' = \frac{1}{m} \left( -m \cdot g + D \cdot v^2 \right ) \\ v' = \frac{D}{m} \left( -m \cdot g / D + v^2 \right ) \\ v' = \frac{D}{m} \left( v^2 - \sqrt{m \cdot g / D }^2\right )$

og

$\\ v'=\frac{D}{m}\cdot\left(v^2 - k^2 \right ) \\ \frac{dv}{dt}=\frac{D}{m}\cdot\left(v^2 - k^2 \right ) \\ \frac{dv}{dt}\frac{1}{v^2 - k^2 }=\frac{D}{m} \\ \int \frac{dv}{dt}\frac{1}{v^2 - k^2 } dt= \int \frac{D}{m} dt$

Kan du måske forklare, hvad du gør i hvert step??

Og er de alle sammen 'svar' på b'eren??

Brugbart svar (0)

Svar #10
18. marts kl. 13:41 af jl9

Det er kun b). Prøv og studer det lidt og om det kan forstås. Fra 1. linje til 2. linje f.eks. divideres der egentlig bare med m på begge sider af lighedstegnet.

Har du lavet a) ?

Svar #11
18. marts kl. 13:43 af Rebecca1234a

nej, ikke endnu

Brugbart svar (0)

Svar #12
18. marts kl. 19:58 af Eksperimentalfysikeren

Bemærk at:

$\frac{e^{s}-e^{-s}}{e^{s}+e^{-s}} = tanh(s)$

tanh står for tangens hyperbolsk

Svar #13
19. marts kl. 11:06 af Rebecca1234a

#12
Bemærk at:

$\frac{e^{s}-e^{-s}}{e^{s}+e^{-s}} = tanh(s)$

tanh står for tangens hyperbolsk

Jeg forstår ikke hvor du får det der fra??

Brugbart svar (0)

Svar #14
19. marts kl. 12:39 af jl9

Der står noget om hyperbolske funktioner her https://da.wikipedia.org/wiki/Hyperbolske_funktioner

Det ser ikke ud til at være en del af opgaveformuleringen i dit projekt, men kunne være sejt at runde opgave f) af med at skrive udtrykket på tanh() formen.

Brugbart svar (0)

Svar #15
19. marts kl. 19:57 af Eksperimentalfysikeren

Der findes nogle funktioner, der svarer til de trigonometriske funktioner. De trigonometriske funktioner er defineret ud fra enhedscirklen. På samme måde som (cos(t),sin(t)) er parameterfremstilling for enhedscirklen, er (cosh(t),sinh(t)) parameterfremstillingen for en hyperbelgren, der har y=x og y=-x som assymptoter. Det viser sig, at cosh(t) = ½(exp(t)+exp(-t)) og sinh(t) = ½(exp(t)-exp(-t)). tanh(t) = sinh(t)/cosh(t).

Skriv et svar til: Udledning af dette udtryk

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.