Matematik

MAT A 2023 MAJ opgave forklaring?

22. maj 2023 af Guleroden1 - Niveau: A-niveau

Hej, så har der været skriftlig eksamen i mat A i dag, og jeg vil lige høre hvordan i al verden man beregner

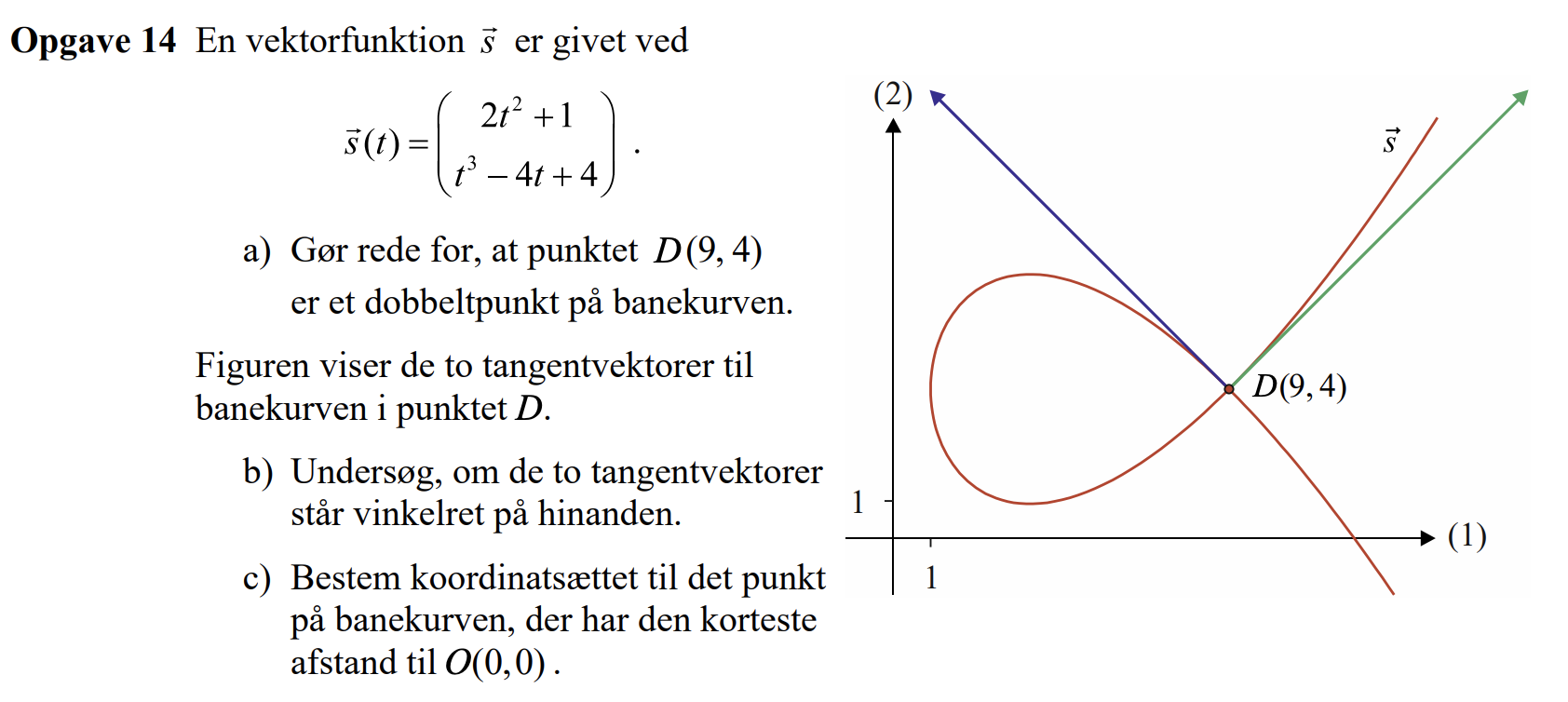
c) i denne opgave?

Tak!

Vedhæftet fil: Skærmbillede 2023-05-22 kl. 16.30.26.png

Brugbart svar (0)

Svar #1
22. maj 2023 af mathon

Brugbart svar (0)

Svar #2
22. maj 2023 af mathon

$\small \begin{array}{lllll}\textbf{a)}\\&&\overrightarrow{s}(t)=\begin{pmatrix} x\\y \end{pmatrix}=\begin{pmatrix} 2t^2+1\\t^3-4t+4 \end{pmatrix}\\\\&\textup{Dobbeltpunkt kr\ae ver:}\\&& \textup{solve}\left (9=2t^2+1 \textup{ and } t^3-4t+4=4,t \right )\\\\&& t=\left\{\begin{matrix} -2\\2 \end{matrix}\right. \end{array}$

Svar #3
22. maj 2023 af Guleroden1

#2
$\small \begin{array}{lllll}\textbf{a)}\\&&\overrightarrow{s}(t)=\begin{pmatrix} x\\y \end{pmatrix}=\begin{pmatrix} 2t^2+1\\t^3-4t+4 \end{pmatrix}\\\\&\textup{Dobbeltpunkt kr\ae ver:}\\&& \textup{solve}\left (9=2t^2+1 \textup{ and } t^3-4t+4=4,t \right )\\\\&& t=\left\{\begin{matrix} -2\\2 \end{matrix}\right. \end{array}$

Ja det var nu mere til opgave C)

Brugbart svar (1)

Svar #4
22. maj 2023 af peter lind

Find minimum for funktionen s(t)2 = (2t²+1)² + (t³-4t+4)²

Brugbart svar (0)

Svar #5
22. maj 2023 af mathon

$\small \begin{array}{llllll} \textbf{b)}\\&& \overrightarrow{s}{\, }'(t)=\begin{pmatrix} 4t\\3t^2-4 \end{pmatrix}\\\\& \textup{Parameterligning}\\& \textup{for tangenter:}\\&& \begin{pmatrix} x\\y \end{pmatrix}=\begin{pmatrix} 9\\4 \end{pmatrix}+p\cdot \begin{pmatrix} 4t\\3t^2-4 \end{pmatrix}\qquad p\in\mathbb{R}\\\\& \textup{dvs tangenterne}\\&\textup{i }D\textup{:}\\&& \begin{pmatrix} x\\y \end{pmatrix}=\begin{pmatrix} 9\\4 \end{pmatrix}+p\cdot \begin{pmatrix} 4\cdot \left (-2 \right )\\3\cdot \left (-2 \right )^2-4 \end{pmatrix}\\\\&& \begin{pmatrix} x\\y \end{pmatrix}=\begin{pmatrix} 9\\4 \end{pmatrix}+p\cdot \begin{pmatrix} -8\\8 \end{pmatrix}\\\\&\textup{og}\\&& \begin{pmatrix} x\\y \end{pmatrix}=\begin{pmatrix} 9\\4 \end{pmatrix}+p\cdot \begin{pmatrix} 4\cdot 2 \\3\cdot 2 ^2-4 \end{pmatrix}\\\\&& \begin{pmatrix} x\\y \end{pmatrix}=\begin{pmatrix} 9\\4 \end{pmatrix}+p\cdot \begin{pmatrix} 8 \\8 \end{pmatrix} \end{array}$

Brugbart svar (1)

Svar #6
22. maj 2023 af mathon

$\small \small \begin{array}{llllll}\textbf{ }\\&\textup{Ortogonale tangenter}\\&\textup{kr\ae ver, at skalarproduktet}\\&\textup{af retningsvektorerne = 0:}\\&& \begin{pmatrix} -8\\8 \end{pmatrix}\cdot \begin{pmatrix} 8\\8 \end{pmatrix}=0\\\\&& -8^2+8^2{\color{Red} =}0\\\\&\textup{Tangenterne \textbf{er} ortogonale.} \end{array}$

Brugbart svar (1)

Svar #7
22. maj 2023 af mathon

$\small \begin{array}{llllll}\textbf{c)}\\&\textup{Punktafstand}\\&\textup{til }O(0,0)\textup{:}\\&& d=\sqrt{(x-0)^2+(y-0)^2}=\sqrt{\left (2t^2+1 \right )^2+\left (t^3-4t+4 \right )^2}\\\\&d\textup{ er mindst, }\\&\textup{n\aa r radikanden }R\\&\textup{er mindst.}\\&\textup{dvs \textup{n\aa r}}\\&&\left (t^6-4t^4+8t^3+20t^2-32t+17 \right ){ }'=\\\\&& 6t^5-16t^3+24t^2+40t-32=0\\\\&& \textup{solve}\left (6t^5-16t^3+24t^2+40t-32=0,t \right )\\\\&& t=0.642133 \\\\&\textup{I punktet:}\\&& \begin{pmatrix} x\\y \end{pmatrix}=\begin{pmatrix} 2\cdot 0.642133^2+1\\0.642133^3-4\cdot 0.642133+4 \end{pmatrix}=\begin{pmatrix} 1.82467\\1.69624 \end{pmatrix} \end{array}$

Svar #8
22. maj 2023 af Guleroden1

Mange tak for jeres svar!

Brugbart svar (0)

Svar #9
23. maj 2023 af Eksperimentalfysikeren

Du kan også benytte, at i det punkt, der er nærmest orego, står stedvektoren vinkelret på hastighedsvekoren. Tag skalarproduktet af dem og sæt det lig med 0. Den fremkomne ligning skulle gerne have den samme løsning som i #7.

Brugbart svar (0)

Svar #10
23. maj 2023 af hejlo

Hej Mathon. Har du hele opgavesættet?

Brugbart svar (0)

Svar #11
24. maj 2023 af mathon

#10
Nej.

Skriv et svar til: MAT A 2023 MAJ opgave forklaring?

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.