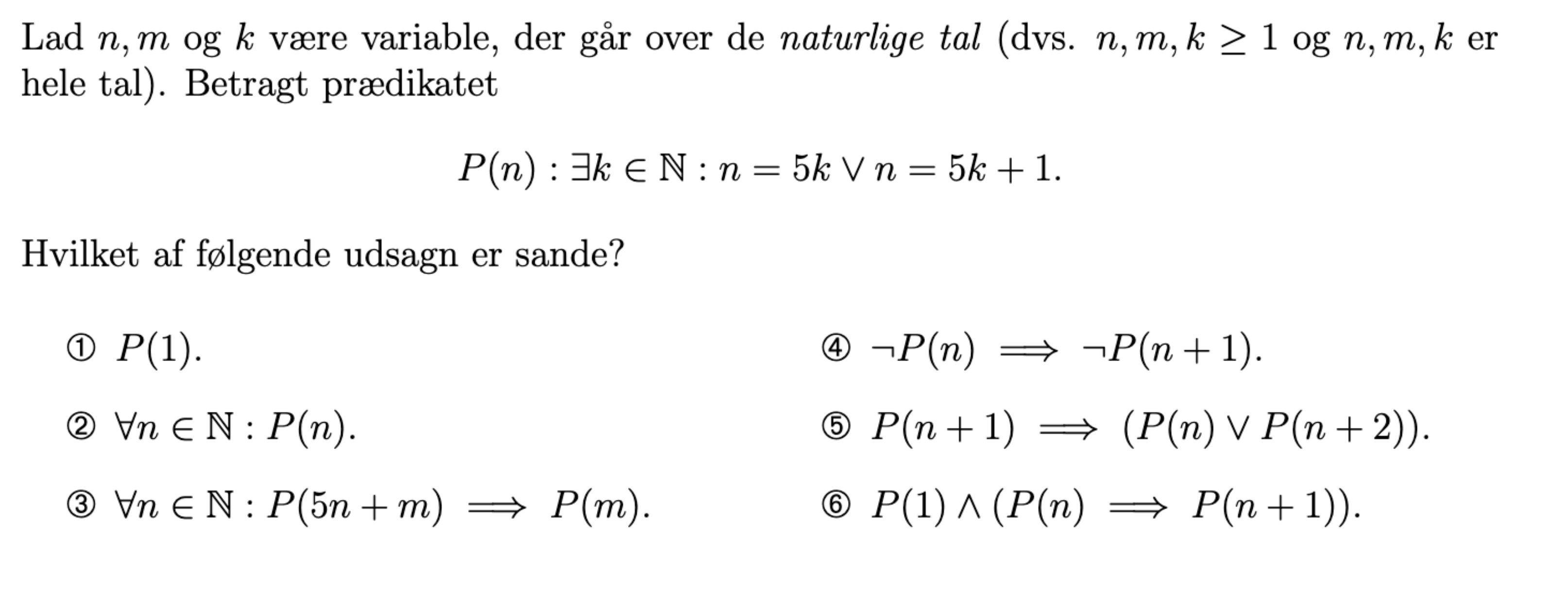Matematik
Prædikat
Jeg skal betragte dette prædikat, og finde hvilket udsagn som er sandt. Dog er jeg i tvivl om hvordan man overhovedet kan finde det, da det siger, at der findes et K i mængden af de naturlige tal, således at n =5k eller n = 5k+1
Men det passer jo ikke hvis n=1?
Svar #1
22. september 2023 af Eksperimentalfysikeren
Nej, så P(1) er falsk. Det er løsningen på første delopgave.
Svar #4
22. september 2023 af M2023
#0. Jeg får, at (3) og (5) er sande?!
(1) er falsk, da der ikke findes et naturligt tal, der ganget med 5 (evt. + 1) giver 1.
(2) er falsk, da P(1) er falsk.
(3) er sand. P(5n+m) er sandt hvis m er et multiplum af 5 eller dette plus 1, hvilket passer til sandheds-mængden for P(n).
(4) er falsk, hvilket følger af modsigelsen: P(4) er falsk, mens P(5) er sand.
(5) er sand. Sandhedsmængden for P(n+1) er 5, 6, 10, 11. Sandhedsmængden for (P(n)∨P(n+2)) er 4, 5, 6, 7, 9, 10, 11, 12. Da den første sandhedsmængde er en delmængde af den anden, så gælder implikationen.
(6) er falsk, fordi P(1) er falsk.
Skriv et svar til: Prædikat
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.