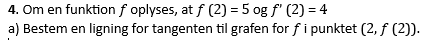Differentialregning

#0 Du ved at den generelle ligning for en tangent er y = f '(x₀)·(x - x₀) + f(x₀). Da det opgaven oplyses at x₀=2, hvorpå f '(2) = 5 og f(2) = 4, kan du omskrive ligningen til den velkendte form y = a·x + b.

Hvordan er det lige man kommer frem til det? Altså skal man sætte 2 ind i tangentligningen og så få svaret derfra?

#2 Ja, dvs. du får ligningen y = f '(2)·(x - 2) + f(2), hvilket du kan omskrive på formen y =a·x +b, når du nu ved hvad tallene f '(2) og f(2) er.

Okay, tusind tak for hjælpen. Jeg må prøve mig frem.

Fortsat god aften:)

Ligningen for tangenten i punktet (x₀ , y₀) på en kurve kommer af, at hældningskoefficienten
for tangenten er lig med differentialkvotienten til funktionen.
Hældningskoefficienten α for den rette linje er som bekendt   α = (y - y₀)/(x - x₀) .
α og f '(x₀) er lig med hinanden. Isolerer vi y og erstatter α med f '(x₀) , får vi tangentligningen.

4. a)