Virksomhedsøkonomi (VØ el. EØ)

Investering

11. marts kl. 10:41 af HogwartsLoading - Niveau: B-niveau

Hej,
Jeg sidder fast ved denne opgave, og om jeg når frem til den rigtige nutidsværdi.
Spørgsmål: Hvilken type anlæg er udfra en økonomisk betragtning billigst, vurderet ud fra kapitalværdien?

Anlæg 1:
Samlet investering: 35 mio. kr.
Vedligeholdelse: 1 mio. kr. pr. år.
Effektfaktor (kølebehov/elforbrug): 4
(Dvs. 4 kWh kræver 1 kWh el)

Anlæg 2:
Samlet investering: 25. mio. kr.
Vedligeholdelse: 1,5 mio. kr. pr. år
Effektfaktor (kølebehov/elforbrug): 3
(Dvs. 3 kWh kræver 1 kWh el)

Det antages envidere, at:
Kølebehov = 12 GWh/år (1 GHw er lige 1.000.000 kWh.)
Levetid = 15 år
Pris på el = 1,1 kr. pr. kWh
Kalkulationsrente = 8 % p. a.

Ud fra ovenstående vil jeg tage elforbrug + vedligeholdelse som negativ cashflow, og at der ikke er et positivt cashflow baseret på de tilgænglige oplysninger.

Anlæg 1: 12 GWh x 1.000.000 kWh = 12.000.000 kWh/år
12.000.000 kWh / 4 (effekt) = 3.000.000 kWh/år
3.000.000 kWh x 1,1 kr. = 3.300.000 kr. + 1.000.000 (vedligeholdelse) = 4.300.000 kr. i negativ cashflow

Anlæg 2: 12 GWh x 1.000.000 kWh = 12.000.000 kWh/år
12.000.000 kWh / 3 (effekt) = 4.000.000 kWh/år
4.000.000 kWh x 1,1 kr. = 4.400.000 kr. + 1.500.000 (vedligeholdelse) = 5.900.000 kr. i negativ cashflow

Baseret på ovenstående får jeg nutidsværdi til:
Anlæg 1 = -71.805.758 kr.
Anlæg 2 = -75.500.924 kr.

Brugbart svar (0)

Svar #1
11. marts kl. 13:24 af ringstedLC

Vedr. dine beregninger: Man kan ikke gange eller dividere pærer med æbler:

$\begin{align*} \textup{GWh}\cdot \textup{kWh} &\;{\color{Red} \neq }\;\frac{\textup{kWh}}{\textup{\aa r}} &&,\; \textup{GWh} = 10^{\,6}\,\textup{kWh} \Rightarrow 12\,\textup{GWh} = 12\cdot 10^{\,6}\,\textup{kWh} \\ \frac{\textup{kWh}}{4} &\;{\color{Red} \neq}\; \frac{\textup{kWh}}{\textup{\aa r}} \quad,\; \textup{kWh}\cdot \textup{kr} \;{\color{Red} \neq}\; \textup{kr} \\ 3\cdot 10^{\,6}\cdot 1.1 &\;{\color{Red} \neq }\;3.3\cdot 10^{\,6} +1\cdot 10^{\,6} &&,\; 3\cdot 10^{\,6}\cdot 1.1=3.3\cdot 10^{\,6} \end{align*}$ Forslag til opstilling:

$\begin{align*} \textup{Anl\ae g\,1 pr.\,\aa r}:\\ \textup{Pris}_\textup{\,El.}: &\; \frac{12\cdot 10^{\,6}\,\textup{kWh}}{4}\cdot 1.10\,\tfrac{\textup{kr}}{\textup{kWh}} &&= \;\,3.3\;\textup{mio.\,kr} \\ \textup{Vedl.-hold}: &&&= \;\,1.0\;\textup{mio.\,kr} \\ -\textup{Cashflow}: &&&= \;\,4.3\;\textup{mio.\,kr} \end{align*}$

Skriv hvordan du har beregnet nutidsværdierne!

Svar #2
11. marts kl. 13:40 af HogwartsLoading

Se udregninger her i vedhæftning.

Vedhæftet fil:Beregning.docx

Brugbart svar (0)

Svar #3
11. marts kl. 15:45 af ringstedLC

Det ser fornuftigt ud.

Det virker dog underligt at en investering og et betragteligt forbrug ikke har noget afkast.

Nutidsværdien i Excel:

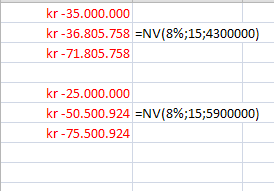
Det billigste anlæg er det med den største (mindst negative) kapitalværdi.

Vedhæftet fil:ScreenShot_20240311153920.png

Svar #4
11. marts kl. 15:49 af HogwartsLoading

Tak for svar.
Rart at vide jeg ikke er på et sidespor :-)

Min udfordring kommer med næste opgave, hvor de beder om, ved hvilken kalkulationsrente de to anlæg har samme kapitalværdi?
Når jeg forsøger med en "What-If" analyse, så får jeg en meget urealistisk rente?

Brugbart svar (0)

Svar #5
11. marts kl. 21:37 af ringstedLC

$\begin{align*} K_1 &= K_2 \\ -35-\frac{4.3}{(1+r)^1}-\frac{4.3}{(1+r)^2}\;...-\frac{4.3}{(1+r)^{15}} &= -25-\frac{5.9}{(1+r)^1}-\frac{5.9}{(1+r)^2}\;...-\frac{5.9}{(1+r)^{15}} \end{align*}$

Vedhæftet fil:ScreenShot_20240311213652.png

Skriv et svar til: Investering

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.