Radioaktivitet

Hvis A har dobbelt så stor aktivitet som B, så er A dobbelt så stor som B. Man kan derfor opfatte A som to eksemplarer af B anbragt sammen. Hvert af disse eksemplarer har samme halveringstid som B. Derfor har A samme halveringstid som B.

De to kilder består af samme stof. Et bestemt stof har én halveringstid, da aktiviteteten aftager eksponentielt.

Situationen svarer til to konti med samme (negative) rente, men forskellig startkapital.

Jeg tror jeg er blevet lidt mere forvirret, jeg må mangle en del forforståelse eller lign.

- Så halveringstiden er betinget af det radioaktive stof der er tale om?

- Og antallet af radioaktive kerner er større hos A end B, hvis A har en større aktivitet?

- Starter man med et mindre antal af radioaktive kerner ved prøve B end ved prøve A?

Hvis antallet af kerner i starten hos prøve B er er større end antallet af kerner ift. antallet af kerner efter 1 halveringstid af prøve A - hvordan kan det være at ved dette start punkt for  antallet af kerner for prøve B, at halvdelen af kerner henfalder efter 1 halveringstid (den samme halveringstid som A), hvis man starter forskellige steder? 

Funktionen A*(½)^t er en funktion der ligyldig hvor du starter fra efter tiden 1 har halveret funktionen

Jeg har også denne opgave:

Hvad er aktiviteten af prøve A sammenlignet med prøve B efter 10 timer?

Jeg skal lige forstå spørgsmålet, bliver der spurgt om hvad aktiviteten er for begge prøver efter 10 timer, eller hvad aktiviteten er for prøve A i starten (og ikke efter 10 timer) sammenlignet med prøve B efter 10 timer? 

#3

- Så halveringstiden er betinget af det radioaktive stof der er tale om?

- Og antallet af radioaktive kerner er større hos A end B, hvis A har en større aktivitet?

- Starter man med et mindre antal af radioaktive kerner ved prøve B end ved prøve A?

Hvis antallet af kerner i starten hos prøve B er er større end antallet af kerner ift. antallet af kerner efter 1 halveringstid af prøve A - hvordan kan det være at ved dette start punkt for  antallet af kerner for prøve B, at halvdelen af kerner henfalder efter 1 halveringstid (den samme halveringstid som A), hvis man starter forskellige steder?    

1) Korrekt. Nogle stoffer halveres ganske hurtigt, for andre tager det tusindvis af år. Det mest kendte er nok kulstof 14, der halveres på 5730 ± 40 år.

2) Ja, da prøverne er det samme stof og aktivititeten er mindre. Eller med andre ord: En stor- og en mindre A-bombe (uran) har forskellige aktivitet, der som bekendt giver strålingssyge forårsaget af radioaktiv stråling.

3) Ja.

4) Halveringstiden er konstant. det vil sige, at uanset hvornår tiden startes vil der til tiden t₀ + T_½ være det halve antal radioaktive kerner tilbage.

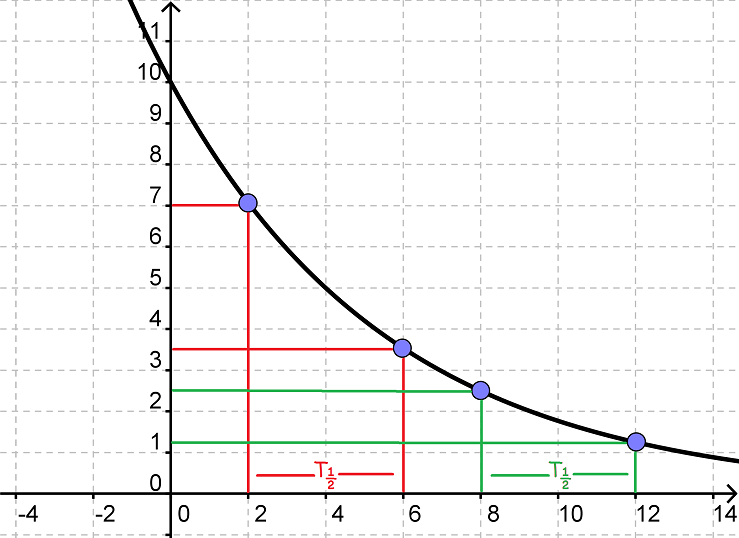
Kilde: https://www.webmatematik.dk/lektioner/matematik-c/funktioner/fordoblings-og-halveringskonstant

Se at y halveres hvergang der gås T_½ frem.

#5 Det er begge prøver efter 10 timer. Ellers havde der stået" af prøve A til tiden t = 0 sammenlignet med... eller lignende.

A har dobbelt så mange kerner som B. Derfor har den dobbelt så stor radioaktivitet. Efter halveringstiden er halvdelen af kernerne henfaldet antallet af tilbageværende kerner er halveret i både A og B. Derfor er A stadigvæk dobbelt så radioaktiv som B.

Efter 10 timer er der henfaldet en bestemt brøkdel af kernerne både i A og i B. Det er den samme brøkdel. Derfor vil A stadig være dobbelt så radioaktiv som B.

Citatet i #5 er tvetydigt. Det skal opfattes som sammenligning af A og B samtidig.

Tak for alle de gode svar alle sammen! :)