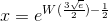Matematik
LambertW?????
Hvorfor er det at når jeg beder Maple om at finde nulpunkter ved
f'(x)=0 så giver den mig et helt latterligt tal at regne med.
Det er en Mat A aflevering og vi er ikke blevet introduceret til e^LambertW endnu, så tror der er noget jeg gør forkert.
Det helt præcise svar jeg får er:
{x = exp(LambertW((3/2)*exp(1/2))-1/2)}
Min funktion er f(x) = x^2*ln(x)-3*x-1
Mallingg
Svar #1
23. juli 2016 af Capion1
Det er meningsløst at begynde at regne på noget, du ikke er introduceret i.
Skal du løse f '(x) = 0 for 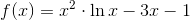 ?
?
Svar #3
24. juli 2016 af Mallingg (Slettet)
Okay, mange tak. Jeg tror det er Maple (Mit matematik program jeg skriver i) som elsker at give præcise svar og dermed også nogle sjove udtryk.
Får tit også RootOf(_Z) som jeg så skal converte til radical tal.
Mallingg
Svar #4
24. juli 2016 af Mallingg (Slettet)
Så det er rigtigt at funktionen kun har nulpunkter 1 sted?
Opgaven fortæller at jeg skal benytte f'(x) til at argumentere for forløbet af grafen for f.
Jeg tænkte at fortegnsundersøgelse via. monotoniforhold kunne klarer dette? Er der andre muligheder der ville være nemmere?
Mallingg
Skriv et svar til: LambertW?????
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.