Talteori find alle positive heltal

Tip: xⁿ-1 kan divideres med x-1.

#1

Tip: xⁿ-1 kan divideres med x-1.

Ok, så fås:

Hvad skal jeg gøre herfra, og jeg er forresten lidt i tvivl om division er muligt når (x-1)=0?

y² = (x⁵-1) : (x-1) = (x-1)⁴
y = (x-1)²

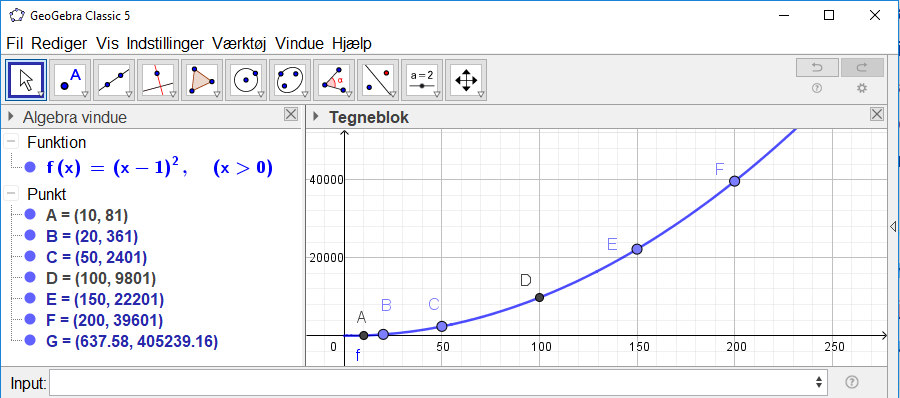
For eksempel         (10,81)  eller  (100,9801).
Men hvordan man udvælger man heltal.?

#3

y² = (x⁵-1) : (x-1) = (x-1)⁴
y = (x-1)²

Så vidt jeg kan se, så er 

Det er klart, at er en løsning for alle , idet vi får nul på begge sider af lighedstegnet, hvis vi sætter . For kan vi dividere igennem med , hvilket giver

.

Jeg ved ikke, hvordan man fortsætter herfra, men jeg kan se, at er en løsning.

#7

Det er klart, at er en løsning for alle , idet vi får nul på begge sider af lighedstegnet, hvis vi sætter . For kan vi dividere igennem med , hvilket giver

.

Jeg ved ikke, hvordan man fortsætter herfra, men jeg kan se, at er en løsning.

Jeg har også fået , men ligesom dig ved jeg ikke, hvordan man fortsætter. Kunne forestille mig, at man kunne gøre brug af modulo men ved ikke, hvordan dette kan gøres.

# 0
Læg mærke til, at # 1 lader antyde, y² isoleres og er lig med summen i en kvotientrække.

#8 Man kunne sagtens forestille sig, at man skulle regne modulo et primtal, men jeg kan ikke lige se løsningen.

Tag kvadratroden på begge sider.
Kvadratroden af  højresiden er  (x-1)²

#11

Tag kvadratroden på begge sider.
Kvadratroden af  højresiden er  (x-1)²

Så vidt jeg forstår, så hentyder du til at . Det kan jeg ikke få til at passe.

For at se hvad der sker med  når x bliver stor, så kan man transformere den, tage en taylor-udvikling, og anvende den omvendte transformation på taylor-udviklingen.

Transformationen herunder er at gange med  og substituere , dvs.

Taylorudviklingen af 2. grad for  om  med Lagrange's restled er

Transformer u tilbage til x ved  

Gang med x²

Dvs.  kan beregnes som x² (heltal) + x/2 (hel eller halv) + de røde led, som hverken er hel eller halv, når , da den tredjeafledede er positiv med maximum 2.57 over [ 0 , 1/4 ].
Dvs. de røde led giver tilsammen noget i intervallet:
  

#13

For at se hvad der sker med  når x bliver stor, så kan man transformere den, tage en taylor-udvikling, og anvende den omvendte transformation på taylor-udviklingen.

Transformationen herunder er at gange med  og substituere , dvs.

Taylorudviklingen af 2. grad for  om  med Lagrange's restled er

Transformer u tilbage til x ved  

Gang med x²

Dvs.  kan beregnes som x² (heltal) + x/2 (hel eller halv) + de røde led, som hverken er hel eller halv, når , da den tredjeafledede er positiv med maximum 2.57 over [ 0 , 1/4 ].
Dvs. de røde led giver tilsammen noget i intervallet:
  

Må ærligt talt indrømme, at jeg ikke har lært om dette, og kan derfor ikke se, hvordan det kan anvendes.

Ignorer dette..

#13: Denne metode ser fornuftig ud. Det kan godt virke lidt indviklet, men det virker. Det er ikke altid enkelt at løse Diofantiske ligninger.

#9: Korrekt. Ligningen (xⁿ-1)(x-1) = x^n-1+x^n-2+...+x+1 kender jeg fra polynomiers division. Jeg ved ikke, om der stadig undervises i det i gymnasiet, men det kan til tider være et nyttigt redskab.

(x , y) = (3 , 11)  tilfredsstiller ligningen.
 

#17

(x , y) = (3 , 11)  tilfredsstiller ligningen.
 

Yep. Dette pointerede #7 også. Har nu løst opgaven og samtidigt vist, at der ikke er flere løsninger end dem angivet i #7.

Det er muligt at give et elementært bevis for, at er den eneste ikke-trivielle løsning. Antag at med og . Så kan vi skrive på formen med . Der gælder så

.

Ved at betragte koefficienten til indser vi, at , og der gælder derfor

.

På den anden side er , og der må derfor gælde samt (idet ). Heraf følger, at , og dermed at .

#19 Hvorfor er  og  nødvendig? Det er jo kun for et enkelt fastlagt , at de to udtryk for  skal være det samme, hvilket de bliver med  , som opfylder  hvis bare .

 viser at  skal være heltallig, men hvordan ved du at det kun sker hvis  og ?