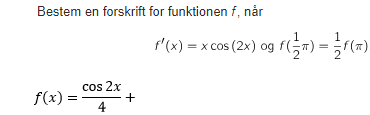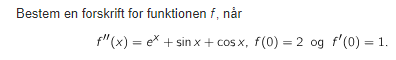Matematik

Bestem en forskrift funktionen f.

17. januar 2019 af Larsdk4 (Slettet) - Niveau: A-niveau

Idet at min egen lære ikke kan svare, mig på mit spørgsmål, Eller med andre ord, han svarer ikke pr e-mail og har fjernundervisning. Derfor hører jer, af hvordan jeg skal komme videre

Vedhæftet fil: Udklip.PNG

Brugbart svar (0)

Svar #1
17. januar 2019 af mathon

Brugbart svar (1)

Svar #2
17. januar 2019 af mathon

$\small f(x)=x\cdot \tfrac{1}{2}\cdot \sin(2x)-\tfrac{1}{2}\cdot \int \sin(2x)\cdot 1\mathrm{d}x=\tfrac{1}{2}x\sin(2x)-\tfrac{1}{2}\cdot \left(-\tfrac{1}{2}\cdot \sin(2x)\right)+C=$

$\small \tfrac{1}{2}x\left (x+\tfrac{1}{2} \right )\sin(2x)+C$

Brugbart svar (0)

Svar #3
17. januar 2019 af mathon

$\small f\left ( \frac{\pi }{2} \right )=\frac{\pi }{4}\cdot \left ( \frac{\pi +1}{2} \right )\cdot \sin(\pi )+C=C$

$\small \tfrac{1}{2}\cdot f\left ( \pi \right )=\tfrac{1}{2}\cdot \left ( \tfrac{\pi }{2}\cdot\left(\pi +\tfrac{1}{2}\right ) \cdot \sin(2\pi )+C\right)=\tfrac{C}{2}$

$\small C=\frac{C}{2}\Leftrightarrow C=0$

konklusion:
$\small \small \small f(x)=\tfrac{1}{2}x \left ( x+\tfrac{1}{2} \right ) \sin(2x)$

Svar #4
17. januar 2019 af Larsdk4 (Slettet)

#2
$\small f(x)=x\cdot \tfrac{1}{2}\cdot \sin(2x)-\tfrac{1}{2}\cdot \int \sin(2x)\cdot 1\mathrm{d}x=\tfrac{1}{2}x\sin(2x)-\tfrac{1}{2}\cdot \left(-\tfrac{1}{2}\cdot \sin(2x)\right)+C=$

$\small \tfrac{1}{2}x\left (x+\tfrac{1}{2} \right )\sin(2x)+C$

Tak for dit hurtige svar :)

Svar #5
17. januar 2019 af Larsdk4 (Slettet)

Mulighed for, at du kan hjælpe med denne opgave ?

Vedhæftet fil:Udklip.PNG

Brugbart svar (0)

Svar #6
17. januar 2019 af mathon

Brugbart svar (0)

Svar #7
17. januar 2019 af mathon

$\small f{\, }'(x)=e^x-\cos(x)+\sin(x)+C_1$

$\small f{\, }'(0)=e^0-\cos(0)+\sin(0)+C_1=1-1+0+C_1=1$ ?

$\small C_1=1$
hvoraf:
$\small f{\, }'(x)=e^x-\cos(x)+\sin(x)+1$

$\small f(x)=e^x-\sin(x)-\cos(x)+x+C_2$

$\small f(0)=e^0-\sin(0)-\cos(0)+0+C_2=2$

$\small 1-0-1+C_2=2$

$\small \small C_2=2$

hvoraf:
$\small f(x)=e^x-\sin(x)-\cos(x)+x+2$

Skriv et svar til: Bestem en forskrift funktionen f.

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.