Matematik
Differentialligninger
Hej. Er der nogle, der vil hjælpe med disse opgaver?
Svar #4
24. januar 2020 af AMelev
#0
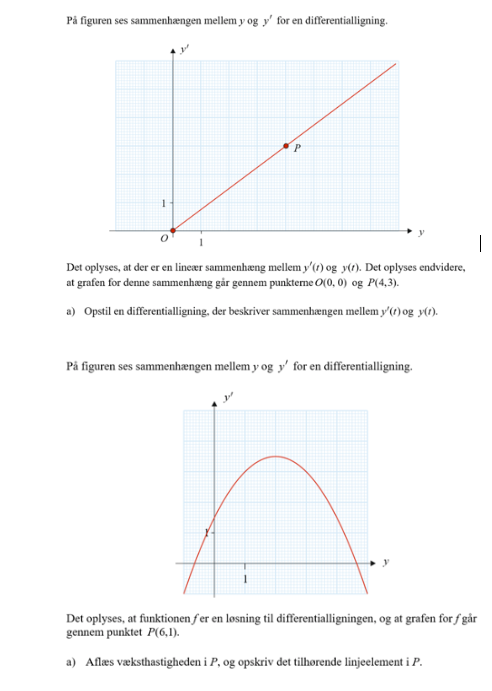
1. opgave Lineær funktion gennem (0,0) og (4,3) er z = 3/4u, så y' = 3/4y
2. opgave P(6,1), dvs. x = 6 og y = 1
Iflg grafen er y'|(y=1) = 3, så væksthastigheden i P er 3
Linjeelementet i P er dermed (6,1,3)
Ad #3 udgangspunktet her er, at y' er afbildet som funktion af x, og ikke som det faktisk er tilfældet som funktion af y, så derfor kan det ikke anvendes.
NB! Husk én tråd pr. opgave, elllers bliver det let noget roderi.
Skriv et svar til: Differentialligninger
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.