2D vektorer

Ja, naturligvis kan de det, dog ikke alle sammen.

Kan du mon komme på nogen vektorer, som aldrig vil skære hinanden i et punkt?

Ja. To (eller flere) ikke-parallelle vektorer vil krydse hinanden. Husk, at når du ser en vektor tegnet, ses kun én repræsentant for vektoren. Selve vektoren er global og ligger derfor alle vegne i dit system, - med kun sin retning og sin længde.

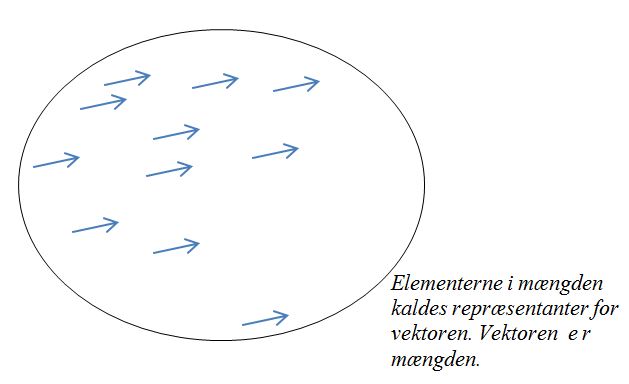
Man kan illustrere vektorbegrebet med et diagram.
Lad  være et orienteret linjestykke.
 er da mængden

Tak for svarerne

Til Capion1: Så vektorer er mængder, indeholder orienterede linjestykker - ka' man ikke bare kalde dem for pile? Er der andre linjestykker som har en orientering? Hvis to mængder overlapper hinanden, så vil mindst én linjestykke fra hver, vil krydse hinanden.Er det rigtigt?

Det er vigtigt at kunne se forskel på  og a ,    a ∈   ( samme længde, samme retning).
 er stedet, hvor repræsentanten a er beliggende i planen, når det orienterede linjestykke
har sit udgangspunkt i O og endepunkt i A.  kan ikke flyttes, men a kan være beliggende hvor som helst
i planen og vil fuldstændig fylde planen ud.
To ikke-parallelle vektorer's repræsentanter vil gennemskære hinanden overalt i planen. 

Tak Capion1

#5 Jeg ved ikke, om jeg er helt enig i, at man skal skelne, men i hvert fald kan jeg ikke forstå, at a ∈  - bør det ikke være  iflg. din skelnen?

#7 Jeg har forstået det som at a er den pil som er en repræsentant for mængden OA også kaldet en vektor - a er en blandt mange pile, der har samme længde og retning som vektoren OA indeholder. Er det ikke rigtigt?

Pas. Jeg opfatter bare a som en anden skrivemåde for , altså vektoren med uendeligt mange repræsentanter.