Matematik

parameter fremstilling

17. september 2020 af andre243g - Niveau: B-niveau

Hejsa,

Har disse to delopgaver, jeg ikke forstår hvordan skal løses helt præcis. Er dog med på, at parameter fremstillingen skal tages i brug. Dog ved jeg ikke hvordan, jeg skal stille ligningerne op.

Har vedhæftet figuren.

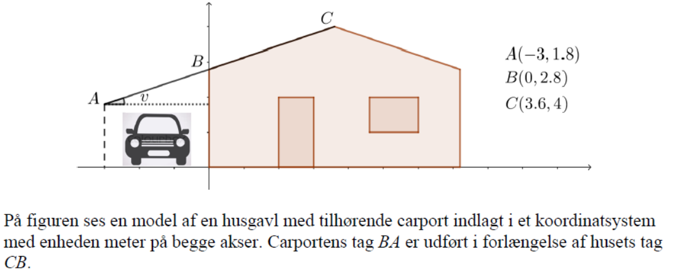
c) Redegør for, at husets og carportens tag er en del af samme rette linje

d) På carportens tag, skal hældningsvinklen v bestemmes.

Vedhæftet fil: Skærmbillede 2020-09-17 193725.png

Brugbart svar (0)

Svar #1
17. september 2020 af peter lind

Brugbart svar (0)

Svar #2
17. september 2020 af peter lind

c) Hvis du har ligningen for linjen B og C er det kun at eftervise at B's koordinater opfylder ligningen. C's z koordinat kan godt sættes til 8

d) tan(v) er linjens hældning

Hvis du ikke har linjens ligning kan du finde den

Brugbart svar (0)

Svar #3
17. september 2020 af mathon

$\small \begin{array}{llll}c)\\& \begin{array}{llll} \textup{linjen gennem A og B:}\\& \begin{array}{llll} \frac{y-1.8}{x-(-3)}=\frac{2.8-1.8}{0-(-3)}\\\\ y-1.8=(x+3)\cdot \frac{1}{3}\\\\ y=\frac{1}{3}x+2.8 \end{array}\\ \textup{Det unders\o ges}\\ \textup{om C's koordinater}\\ \textup{g\o r ligningen sand:}\\& \begin{array}{llll} \frac{1}{3}\cdot 3.6+2.8=4 \end{array}\\ \textup{hvilket er tilf\ae ldet.} \end{array}\end{array}$

Brugbart svar (0)

Svar #4
17. september 2020 af mathon

$\small \small \begin{array}{llll}d)\\& \begin{array}{llll} \textup{linjens h\ae ldning:}\\& \begin{array}{llll} \tan(v)=\frac{1}{3}\\\\ v=\tan^{-1}\left ( \frac{1}{3} \right )=18.43\degree \end{array} \end{array}\end{array}$

Svar #5
17. september 2020 af andre243g

Tak for hjælpen!

Brugbart svar (0)

Svar #6
18. september 2020 af mathon

$\small \begin{array}{lllll} \textup{parameterfremstilling:}&\overrightarrow{OP}=\overrightarrow{OA}+t\cdot \overrightarrow{AB}\qquad t\in\mathbb{R}\\\\ \textup{retningsvektor:}&\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}=\begin{pmatrix} 0\\2.8 \end{pmatrix}-\begin{pmatrix} -3 \\ 1.8 \end{pmatrix}=\begin{pmatrix} 3\\1 \end{pmatrix}\\\\ \textup{N\aa r det variable }\\ \textup{punkt er } P(x,y)\\ \textup{haves:}&\begin{pmatrix} x\\y \end{pmatrix}=\begin{pmatrix} -3\\1.8 \end{pmatrix}+t\cdot \begin{pmatrix} 3\\1 \end{pmatrix} \quad t\in\mathbb{R}\end{array}$

Svar #7
18. september 2020 af andre243g

#3
$\small \begin{array}{llll}c)\\& \begin{array}{llll} \textup{linjen gennem A og B:}\\& \begin{array}{llll} \frac{y-1.8}{x-(-3)}=\frac{2.8-1.8}{0-(-3)}\\\\ y-1.8=(x+3)\cdot \frac{1}{3}\\\\ y=\frac{1}{3}x+2.8 \end{array}\\ \textup{Det unders\o ges}\\ \textup{om C's koordinater}\\ \textup{g\o r ligningen sand:}\\& \begin{array}{llll} \frac{1}{3}\cdot 3.6+2.8=4 \end{array}\\ \textup{hvilket er tilf\ae ldet.} \end{array}\end{array}$

Er dette linjens ligning?

Brugbart svar (0)

Svar #8
18. september 2020 af mathon

Ja.

Skriv et svar til: parameter fremstilling

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.