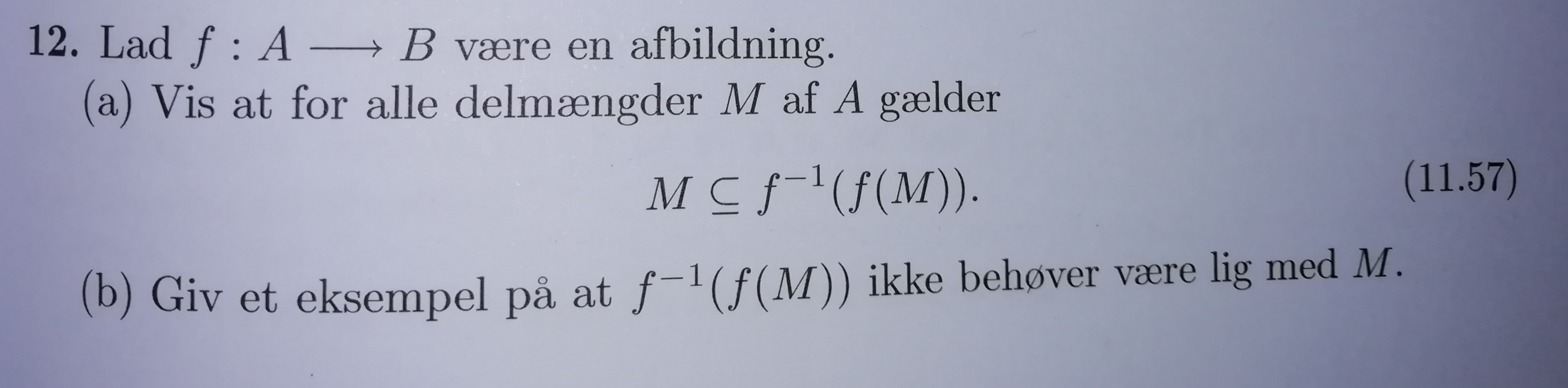Inverse afbildning

#0 (a) Forarbejde: Vi har, at                                                                                                                                                                f(M) = { y | ∃ x ∈ M : y = f(x) } ⊆ B og f^-1(f(M)) = { x | f(x) ∈ f(M)} ⊆ A                                                 desuden er M ⊂ A. Der skal vises implikationen                                                                                                                                                              x ∈ M ⇒ f(x) ∈  f(M).                                                                                    Dvs. tages et x, skal dets billede ligge i f(M), men det gør den per definition. Ellers ville det ligge i en               anden mængde af B, hvilket er nonsens. Det må betyde, at x ... så ligger den ønskede mængde!!!

           Bevis: Lad x ∈ M, hvor M er en vilkårlig delmængde af A. Da er f(x) ∈ f(M). Derfor følger det, at                                   x ∈  f^-1 (f(M)  som ønsket.                                     

#0 (b) Kun forarbejde:                                                                                                                                                      Tilsyneladende gælder der generelt, at M ≠ f^-1(f(M)), idet der eksempler (flertal???)                                             på, at inklusionen  f^-1(f(M)) ⊆ M ikke gælder. Vi prøver at lave et enkelt eksempel. Hvis                                     A = {x,y,z} og B ={1,2,3} således at x → f(x) =2, y → f(y) = 2 og z → f(z) = 3. Mængden M                                 skal være en delmængde af A ... Vi prøver med M = {y} - en singleton. Hvad så? Så må                                     f(M) = {2} og f^-1(f(M)) = f^-1({2}) = {x,y} ≠ {y}. Ja, vores eksempel dur!                                                                                                                                                                                                             

Tusind tak!!!