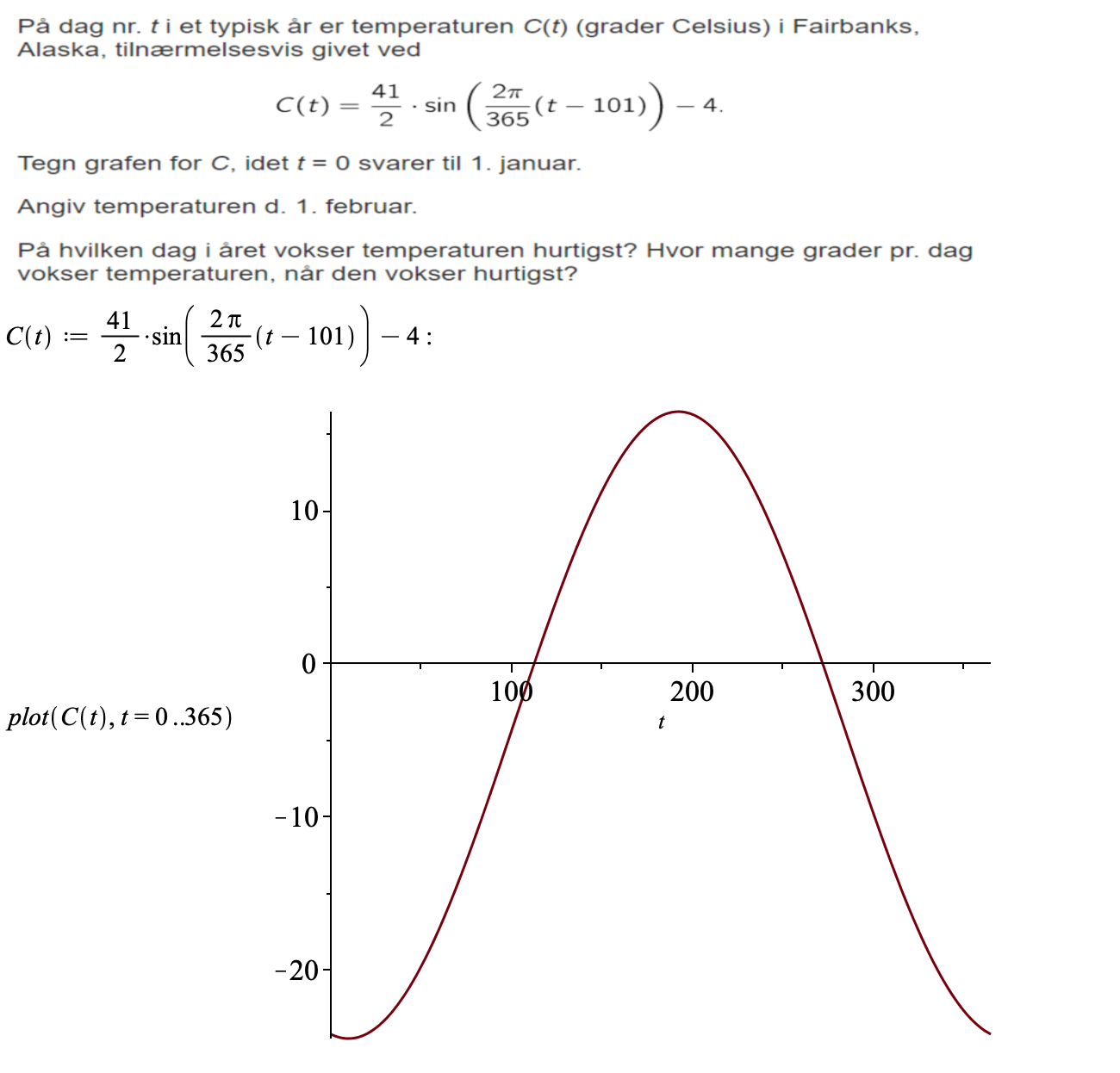
Matematik

Harmonisk svining

21. januar 2021 af dennis13434 - Niveau: B-niveau

Hej

Har vedlagt min opgave samt graf

Jeg har brug for hjælp til den sidste del af opgaven

Mit bud er at den dag temperaturen vokser mest, er omkring 11.Maj.

Vedhæftet fil: Skærmbillede 2021-01-21 kl. 23.07.06.png

Brugbart svar (0)

Svar #1
21. januar 2021 af peter lind

det er når indmaden i sinusfunktionen er 0

Brugbart svar (0)

Svar #2
21. januar 2021 af ringstedLC

t = 101. Tjek lige kalenderen igen.

Svar #3
21. januar 2021 af dennis13434

Så dag 116?

Svar #4
21. januar 2021 af dennis13434

Og hvorfor egentlig

Svar #5
21. januar 2021 af dennis13434

Opfølgende spg.

Hvordan vil man beregne væksten fra dag til dag?

Er det ved at tage fx C(121)-C(120) ?

mvh

Brugbart svar (0)

Svar #6
21. januar 2021 af ringstedLC

#3: Nej, dag 101.

#4: Grafen for C(t) viser temp. Det vil sige, at hældningen er C '(t). Hældningen er størst, når:

$\begin{align*} C^{\,''}\!(t)=C^{\,'}\!\Bigl(C^{\,'}(t)\!\Bigr) &= 0\Rightarrow t\approx 101 \end{align*}$

#5: Det kunne du gøre. Men stigningen er jo også C '(t₀), altså hældningen af en tangent i (t₀, C(t₀))

Svar #7
21. januar 2021 af dennis13434

Kan du forklare dit svar til #4

Tak for hjælpen.

Svar #8
22. januar 2021 af dennis13434

Hvordan kan man formulere #6. Hvad betydet det?

Brugbart svar (0)

Svar #9
24. januar 2021 af ringstedLC

#6: Rettelse for svar til #5:

$\begin{align*} \text{Stigning}_{\,t=120} &= \frac{C(t_{121})-C(t_{119})}{t_{121}-t_{119}} \end{align*}$

Brugbart svar (0)

Svar #10
24. januar 2021 af ringstedLC

#7: Hvis du skulle finde ud af, hvornår temperaturen var størst, altså C_maks., ville du sikkert differentiere og løse:

$\begin{align*} C(t) &= A\cdot \sin\left (\tfrac{2\pi}{365}\cdot (t-1)\right )+K \;,\;0\leq t\leq 365 \\ C{\,'}(t)=0 &= A\cdot k_1\cdot \cos\bigl(\text{Indmad}_{\sin}\bigr) \\ 0 &= \cos\bigl(\text{Indmad}_{\sin}\bigr)\Rightarrow \text{Indmad}_{\sin}=\;?\Rightarrow t=\;? \end{align*}$

Når du her skal bestemme, hvornår temp.-stigningen er størst, kan samme metode anvendes:

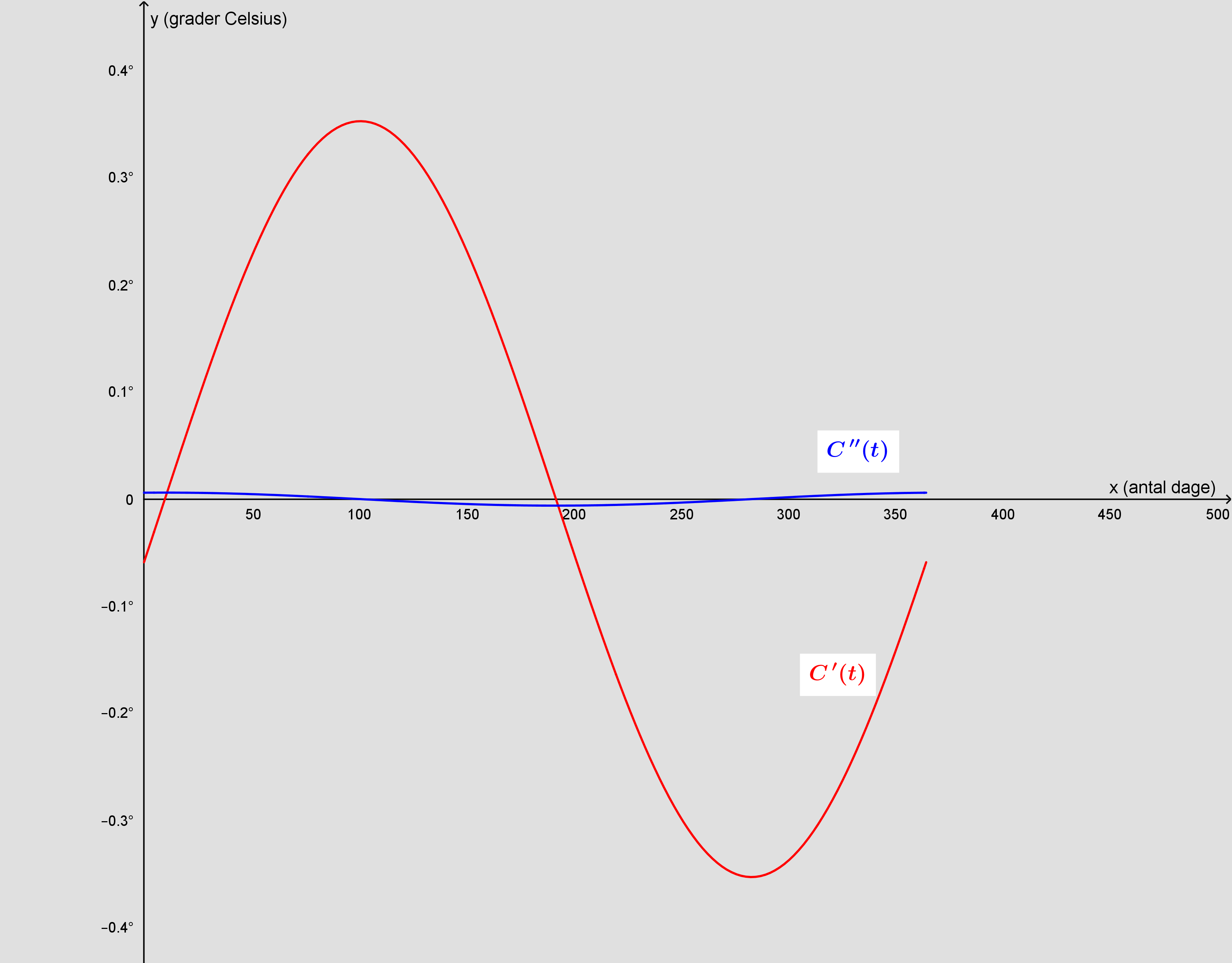
$\begin{align*} C{\,'}(t) &= A\cdot k_1\cdot \cos\bigl(\text{Indmad}_{\sin}\bigr)\;,\;0\leq t\leq 365 \\ C{\,''}(t)=0 &= A\cdot k_1\cdot k_2\cdot \sin\bigl(\text{Indmad}_{\sin}\bigr) \\ 0 &= \sin\bigl(\text{Indmad}_{\sin}\bigr)\Rightarrow \text{Indmad}_{\sin}=\;?\Rightarrow t=\;? \end{align*}$

Bemærk opløsningen på y-aksen, hvis du vil tegne graferne.

Vedhæftet fil:_0.png

Skriv et svar til: Harmonisk svining

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.