Matematik

Integral

28. februar 2021 af javannah5 - Niveau: A-niveau

Jeg gik resultatet til at være 3,71 men hvordan skal en geometrisk fortolkning af dette resultat se ud?

Vedhæftet fil: 85EB9055-508E-4D77-8A3C-945B17262A7F.jpeg

Brugbart svar (0)

Svar #1
28. februar 2021 af mathon

Brugbart svar (0)

Svar #2
28. februar 2021 af AMelev

Resultatet angiver arealet af punktmængden, der begrænses af akserne i 1. kvadrant, grafen for f(x) = 8x³ + e^x samt linjen x = 1.

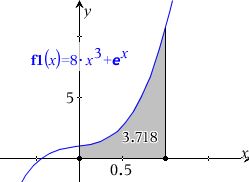
Vedhæftet fil:Udklip.JPG

Brugbart svar (0)

Svar #3
28. februar 2021 af mathon

$\small \begin{array}{lllll} \textbf{a)}\\& \int_{0}^{1} (8x^3+e^x)\,\mathrm{d}x=&\left [ 2x^4+e^x \right ]_{0}^{1}= 2\cdot 1^4+e^1-\left ( 2\cdot 0^4+e^0 \right )=2+e-1=1+e \\\\\\& \textup{Fortolkning:}&\textup{Arealet i 1. kvadrant begr\ae nset af grafen for funktionen }f(x)=8x^2+e^x\\&& \textup{og linjen med ligningen }x=1. \end{array}$

Skriv et svar til: Integral

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.