Musik

Er der nogen der kan lave dem? I GeoGebra

28. maj 2021 af Cecilie567 (Slettet) - Niveau: B-niveau

Vedhæftet fil: Skærmbillede 2021-05-28 152535.png

Brugbart svar (0)

Svar #1
28. maj 2021 af mathon

Brugbart svar (0)

Svar #2
28. maj 2021 af mathon

På det tidspunkt, hvor væksthastigheden er størst, er f(x) = 191.3 / 2
dvs
$\small x=\frac{\ln(9.43)}{0.062}$

Svar #3
28. maj 2021 af Cecilie567 (Slettet)

men efter hvor mange dag?

Svar #4
28. maj 2021 af Cecilie567 (Slettet)

#2
På det tidspunkt, hvor væksthastigheden er størst, er f(x) = 191.3 / 2
dvs
$\small x=\frac{\ln(9.43)}{0.062}$

men erfter hvor mange dag?

Brugbart svar (0)

Svar #5
28. maj 2021 af mathon

$\begin{array}{llllll}\textup{efter } x=\frac{\ln(9.43)}{0.062}=36\;\textup{dage} \end{array}$

Svar #6
28. maj 2021 af Cecilie567 (Slettet)

Er der nogen der kan hjælp med a og b

Brugbart svar (1)

Svar #7
28. maj 2021 af mathon

eller
$\small \begin{array}{llllll}& \textup{Define }f(x)=\frac{191.3}{1+9.43\cdot e^{-0.062\cdot x}}\\\\&\textup{solve}\left (\frac{\mathrm{d} ^2}{\mathrm{d} x^2}f(x)=0,x \right ) \end{array}$

Svar #8
28. maj 2021 af Cecilie567 (Slettet)

#7
eller
$\small \begin{array}{llllll}& \textup{Define }f(x)=\frac{191.3}{1+9.43\cdot e^{-0.062\cdot x}}\\\\&\textup{solve}\left (\frac{\mathrm{d} ^2}{\mathrm{d} x^2}f(x)=0,x \right ) \end{array}$

jag kan dsv. ikke finde ud af det p´å den måde

arbejder kun på GeoGebra

men tak

Brugbart svar (1)

Svar #9
28. maj 2021 af mathon

$\small \small \begin{array}{llllll}&& \textup{Define }f(x)=\frac{191.3}{1+9.43\cdot e^{-0.062\cdot x}}\\\\&&\textup{solve}\left (\frac{\mathrm{d} ^2}{\mathrm{d} x^2}f(x)=0,x \right ) \\\\ \textbf{a)}\\&& f(20)\\\\&&\textup{Define }f_m=\frac{\mathrm{d} }{\mathrm{d} x}(f(x))\\\\&& f_m(20) \end{array}$

Svar #10
28. maj 2021 af Cecilie567 (Slettet)

#9
$\small \small \begin{array}{llllll}&& \textup{Define }f(x)=\frac{191.3}{1+9.43\cdot e^{-0.062\cdot x}}\\\\&&\textup{solve}\left (\frac{\mathrm{d} ^2}{\mathrm{d} x^2}f(x)=0,x \right ) \\\\ \textbf{a)}\\&& f(20)\\\\&&\textup{Define }f_m=\frac{\mathrm{d} }{\mathrm{d} x}(f(x))\\\\&& f_m(20) \end{array}$

er det her rigtige?
eller skal jeg skrive y= 51.3istedet for ?

Vedhæftet fil:erdet.png

Brugbart svar (0)

Svar #11
28. maj 2021 af ringstedLC

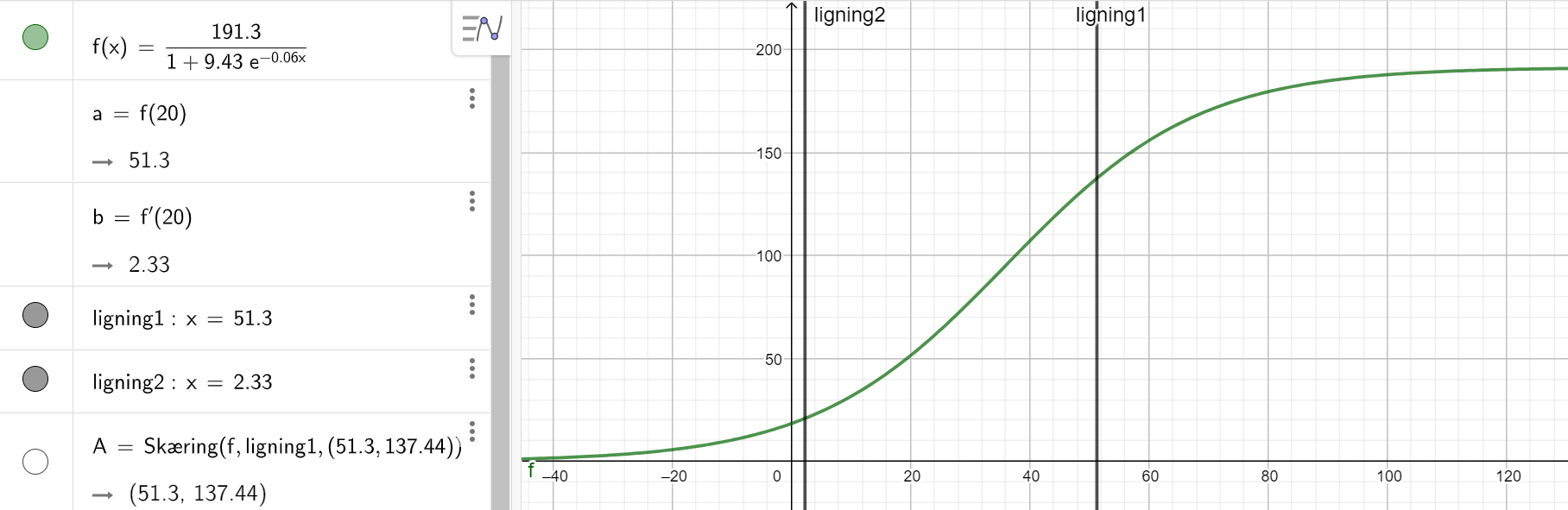
#10: Ja,

$\begin{align*} f(20) &= 51.3 \\ f'(20) &= 2.33 \end{align*}$

I "Input:" skrives: f', 0 ≤ x ≤ 60. Det giver både forskrift og graf.

Når blot "funktion", her f, er defineret og differentiabel, så differentierer GG "funktion", når der skrives "funktion" efterfulgt af '. Det benyttes også med kommandoen f '(20) = a

Skriv et svar til: Er der nogen der kan lave dem? I GeoGebra

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.