Matematik

Definitionsmængde

01. oktober 2021 af gavs (Slettet) - Niveau: Universitet/Videregående

Jeg skal bestemme den størst mulige definitionsmængde i xy-planen for funktionen:

$f(x,y)=\sqrt{5xy-3y^2}$

Jeg har opstillet denne ulighed:

$5xy-3y^2\geq 0\Leftrightarrow \ y\leq \frac{5}{3}x$

Så man får linjen:

$p=\frac{5}{3}x$

Jeg har så angivet definitionsmængden til at være alle de punkter, der i 1. kvadrant i koordinatsystemet ligger under p, og alle de punkter, der i 3. kvadrant ligger over p. Der er ikke nogen punkter i 2. og 4. kvadrant. Er det korrekt?

Brugbart svar (0)

Svar #1
01. oktober 2021 af Soeffi

#0. Ja! Svar i Geogebra nedenfor (uligheden skrives ind i input-feltet og man trykker enter):

Vedhæftet fil:Ulighed.png

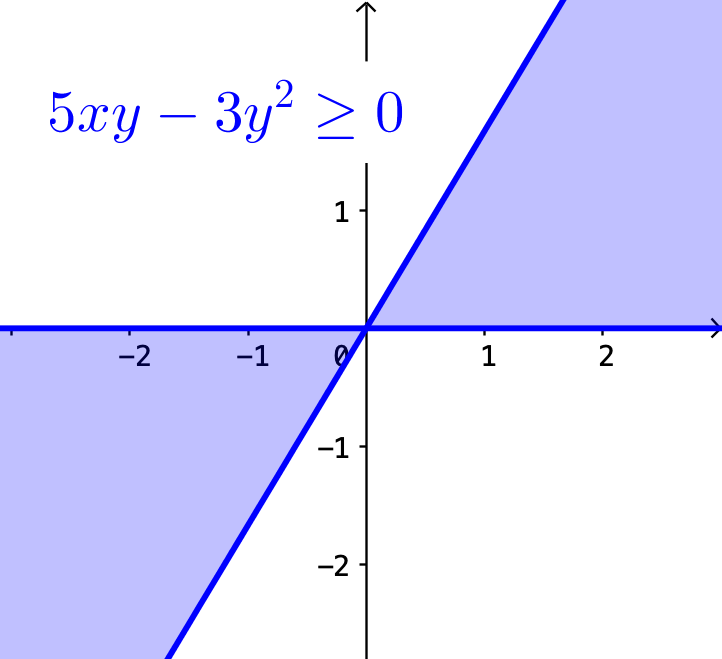
Svar #2
01. oktober 2021 af gavs (Slettet)

Hov. Jeg glemte at skrive, at punkterne på linjen også er med, men tæller punktet (0,0) egentlig med i definitionsmængden?

Brugbart svar (0)

Svar #3
01. oktober 2021 af Soeffi

#2. Prøv at sætte x = 0 og y = 0 ind og se.

Brugbart svar (0)

Svar #4
01. oktober 2021 af LeonhardEuler

Omskriv til ⁵/₃xy≥ y². Betragt nu de to tilfælde hvor y < 0 og 0 ≤ y.

Brugbart svar (0)

Svar #5
01. oktober 2021 af Soeffi

#0. Uligheden løses på følgende måde:

$5xy-3y^2\geq 0\Leftrightarrow y\cdot (5x-3y)\geq 0\Leftrightarrow$

$y\;er\;0 \;eller\; (5x-3y) \;er \;0\; (=)\;eller \;de \;har \;samme \;fortegn\; (>)\Leftrightarrow$

$\\y=0 \\ \vee \\y=\tfrac{5}{3}x\\ \vee \\y>0\wedge y<\tfrac{5}{3}x\\ \vee\\ y<0\wedge y>\tfrac{5}{3}x$

Svar #6
10. oktober 2021 af gavs (Slettet)

Tak for hjælpen. Er det korrekt, at denne mængde er lukket og ubegrænset?

Brugbart svar (0)

Svar #7
10. oktober 2021 af LeonhardEuler

Ja.

Brugbart svar (0)

Svar #8
10. oktober 2021 af Soeffi

#5...

$5xy-3y^2\geq 0\Leftrightarrow y\cdot (5x-3y)\geq 0\Leftrightarrow$

$\\y\;er\;0 \;eller\; (5x-3y) \;er \;0\; (=)\;eller \;y\;og\; (5x-3y)\;har \;samme \;fortegn\; (>) \\\\ \Leftrightarrow$

$\\y=0 \\ \vee \\y=\tfrac{5}{3}x\\ \vee \\y<0\wedge (5x-3y)<0\\ \vee\\ y>0\wedge (5x-3y)>0 \\ \\\Leftrightarrow$

$\\y=0 \\ \vee \\y=\tfrac{5}{3}x\\ \vee \\y<0\wedge y>\tfrac{5}{3}x\\ \vee\\ y>0\wedge y<\tfrac{5}{3}x$

Brugbart svar (0)

Svar #9
10. oktober 2021 af Soeffi

#8...

$\\y=0 \\ \vee \\\textbf{5x-3y=0}\\ \vee \\y<0\wedge (5x-3y)<0\\ \vee\\ y>0\wedge (5x-3y)>0$

...

Skriv et svar til: Definitionsmængde

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.