Matematik
integralregning - HJÆÆLPPP
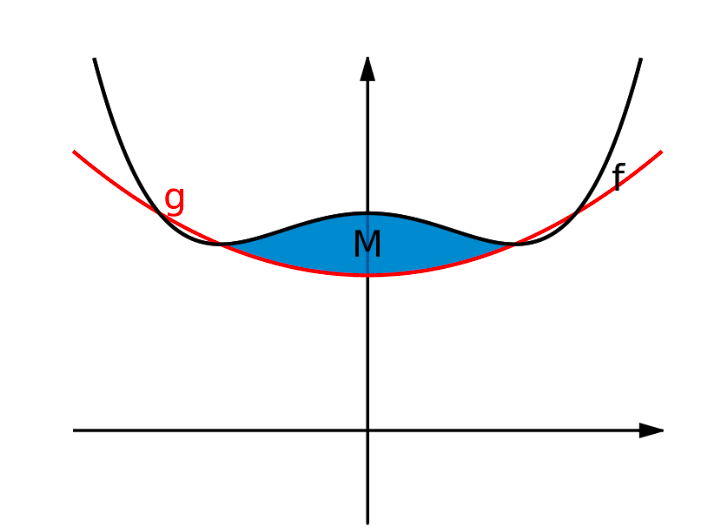
To funktioner er givet ved forskrifterne f(x)=x4−2x2+7 g(x)=x2+5 Tilsammen afgrænser graferne for de to funktioner en punktmængde M på intervallet −1 til 1. Hvad er arealet af M?
normalt ville jeg bare løse ligningen x4−2x2+7-x2+5 i wordmat og få 2 x-værdier, som jeg ville sætte ind i grænseværdiernes plads og integrerer.
men wordmat gider ikke løse den sammensatte ligning, så kan ikke helt finde ud af, hvad de to værdier giver
Svar #2
15. oktober 2021 af ringstedLC
Det fremgår ikke hvilken "sammensat" ligning (det er der ikke noget, der hedder), du vil have Wordmat til at løse, men du skal læse din opgave:
Tip: Start med at reducere integranden.
Svar #3
16. oktober 2021 af Anders521
#0 Du kunne dog løse ligningen f(x) = g(x) i hånden. Du vil nå frem til en "forklædt 2.gradsligning"
x4−3x2+2 = 0. Sæt y = x2 således at y2 - 3y + 2 = 0 Du vil nå frem til flg.: y = 1 ∨ y = -1 hvilket er det samme som x2 = 1 ∨ x2 = -1 Herfra står det klart, at løsningerne til ligningen er -1 og 1, hvilket er dine øvre og nedre grænse. Ud fra figuren står det også klart, at for ethvert x ∈ [ -1; 1 ] er f(x) > g(x). Dermed har du dit bestemte integrale
∫-11 h(x) dx, hvor h(x) = f(x) - g(x)
Svar #5
16. oktober 2021 af Anders521
#4 Ups, selvfølgelig er det x2 = 1 ∨ x2 = 2. Tak for rettelsen.
Hvorfor beregnet noget, der oplyses? Du kan vel læse i #0, at trådskriveren gerne vil løse ligningen (selv om det er ikke er nødvendigt).
Svar #6
16. oktober 2021 af ringstedLC
Nej, jeg læser, at trådstarter gerne vil løse en eller anden ligning-, ikke hvilken. Og da Wordmat ikke finder en løsning, kunne det fx være f(x) = 0
Svar #7
16. oktober 2021 af Anders521
#6 Der skrives i 2. afsnit
"normalt ville jeg bare løse ligningen x4−2x2+7-x2+5 i wordmat normalt og få 2 x-værdier, som jeg ville sætte ind i grænseværdiernes plads og integrerer."
På trods af fejl i opskrivningen af ligningen oa., er det åbenlyst, hvad trådskriveren har i sinde.
Skriv et svar til: integralregning - HJÆÆLPPP
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.