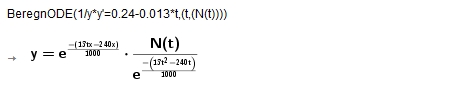Matematik

differentialligning geogebra

17. oktober 2021 af MCS1 - Niveau: A-niveau

Skal jeg bare sige BeregnODE(0,24-0,013*t)

Svar #1
17. oktober 2021 af MCS1

Opgaven

Vedhæftet fil:Screenshot 2021-10-17 021038.png

Brugbart svar (0)

Svar #2
17. oktober 2021 af ringstedLC

Brugbart svar (0)

Svar #3
17. oktober 2021 af ringstedLC

#0: Der sker ikke noget ved at prøve, men der skal jo være en ligning. Og du gives et punkt på grafen.

$\begin{align*} &\textup{Uden\,def.:}\\ &\textup{BeregnODE}\bigl(<\!\textup{ligning}\!>, <\!\textup{Punkt(er)\,p\aa \,f}\!> \bigr) \\ &\textup{BeregnODE}\Bigl(\tfrac{1}{y}\cdot y'=...\,, \bigl(t_0,N(t_0)\bigr)\Bigr) \\ &\rightarrow y=... \\\\ &\textup{Med def.:}\\ &\textup{BeregnODE}\bigl(<\!\textup{ligning}\!>, <\!\textup{afh.\,var.}\!>, <\!\textup{uafh.\,var.}\!>, <\!\textup{Punkt(er)\,p\aa \,f}\!> \bigr) \\ &\textup{BeregnODE}\Bigl(\tfrac{1}{N}\cdot N'=...\,, N,t, \bigl(t_0,N(t_0)\bigr)\Bigr) \\ &\rightarrow N(t)=... \\\\ \end{align*}$

Brugbart svar (0)

Svar #4
17. oktober 2021 af jantand

Hvorfor ikke prøve at løse ligningen.

Ganges med dt på begge sider og integrer. Husk arbitrær konstant c

Svar #5
17. oktober 2021 af MCS1

er det her korrekt

Vedhæftet fil:Screenshot 2021-10-17 131208.png

Brugbart svar (0)

Svar #6
17. oktober 2021 af jantand

Du spørger: er det her korrekt. Hvad mener du?

Svar #7
17. oktober 2021 af MCS1

med af finde forskriften

Brugbart svar (0)

Svar #8
17. oktober 2021 af ringstedLC

Punktet er bestanden i 1992.

Brugbart svar (0)

Svar #9
17. oktober 2021 af jantand

Du har ikke sendt et forslag med, kun et spørgsmål.

Svar #10
17. oktober 2021 af MCS1

Brugbart svar (0)

Svar #11
17. oktober 2021 af jantand

Du får ln1/N= 0,24*t - 0,013* t² + c

Så e^(ln1/N)osv

N= e^{(0,24*t-0,013*(t}²⁾+c ( Det skal være t²)

Du kan sætte de oplysninger ind du har , og dermed finde c

Svar #12
17. oktober 2021 af MCS1

Ja men når jeg prøver at få det lavet i geogebra får jeg noget helt andet

Brugbart svar (0)

Svar #13
17. oktober 2021 af jantand

Så lav det uden geogebra. Så ved du hvad der sker. Jeg bruger papir og blyant.

Svar #14
17. oktober 2021 af MCS1

Opgaven skal laves i geogebra, den må ikke laves i hånden

Brugbart svar (0)

Svar #15
17. oktober 2021 af jantand

Du må da få samme resultat som mig når du integrerer i geogebra.

Brugbart svar (0)

Svar #16
17. oktober 2021 af Soeffi

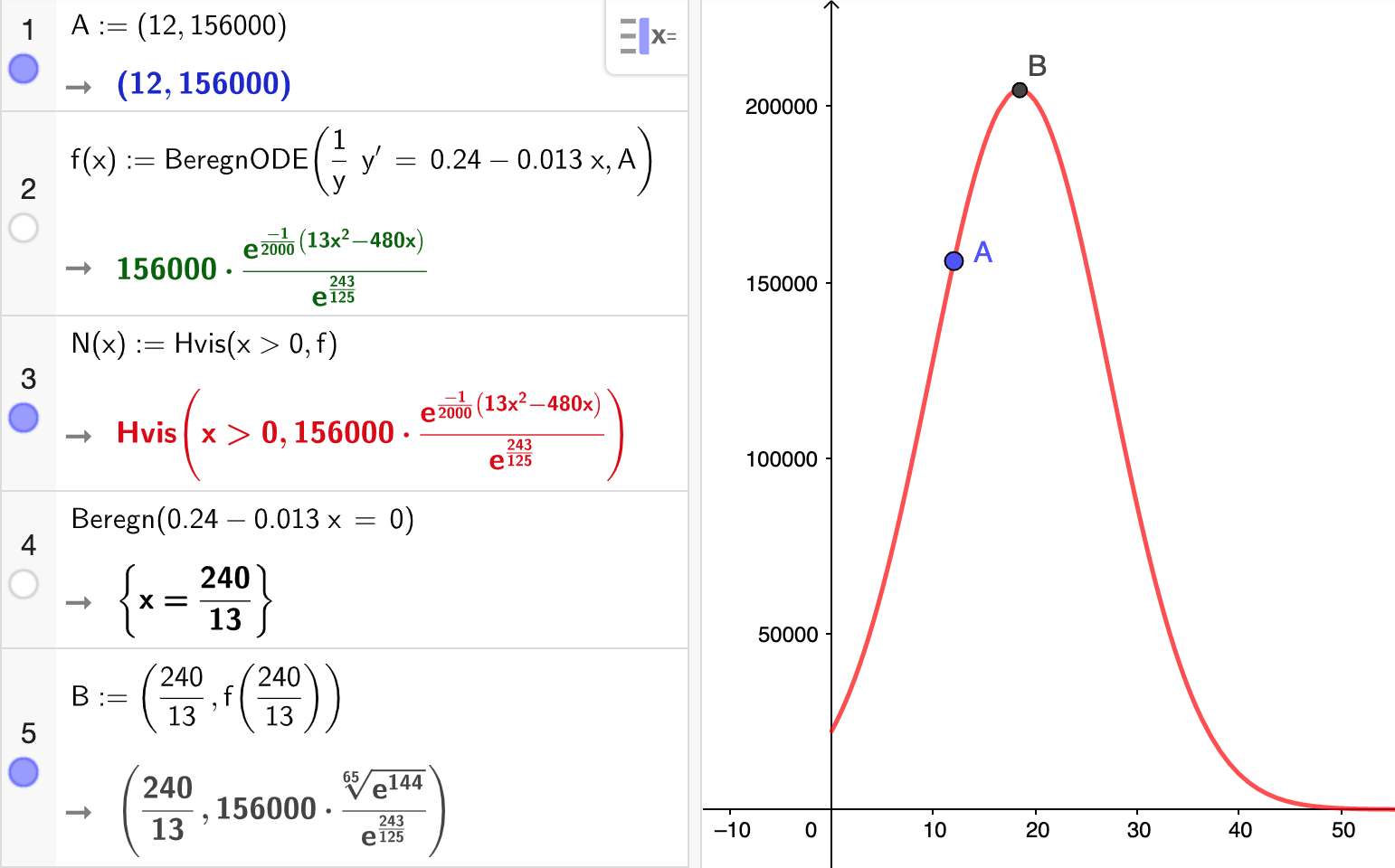
#0. Jeg får følgende: (punktet A er start og B er maksimum)...

Vedhæftet fil:Skærmbillede 2021-10-17 kl. 15.49.12.png

Brugbart svar (0)

Svar #17
17. oktober 2021 af Soeffi

#16...punktet A er 1992...

Skriv et svar til: differentialligning geogebra

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.