Vektor - bevis(k*`#mover(mi("a"),mo("→"))`) . `#mover(mi("b"),mo("→"))` = `#mover(mi("a"),mo("→"))` . (k*`#mover(mi("b&q

Ja, jeg skal lave et bevis for dette, men ved ikke hvordan den vil se ud.

jeg er nemlig i gang med at lave beviser for, at bedre at kunne forstår det.

Benyt at

samt definitionen for skalarprodukt

''Beny at'' hvad?

Hvis det er et billede, kan du så indsætte det på en anden måde, for jeg kan ikke klikke på den, da der bare dukker en størgsmåltegn op?

#3

Benyt at

samt definitionen for skalarprodukt

Hvor er b i denne sammenhæng af dit ''bevis''?

At en skalar ganget på en vektor svarer til at gange skalaren på hver af vektorens koordinater.

Du kan benytte udtrykket sammen med definitionen for skalarprodukt af to vektorer til at skrive beviset op.

Jeg forstår ikke hvordan man præcis gør det med dit billede?

Jeg ahr også en b-værdi og jeg ved ikke andet, at et skalarprodukt er bare ''at man ganger to tal sammen'', men ved ikke hvordan man opskriver et bevis for det?

Skalarproduktet af to vektorer er ikke bare "at man ganger to tal sammen"

#10

Skalarproduktet af to vektorer er ikke bare "at man ganger to tal sammen"

hvad er det så præcist?

Jeg har prøvet, at læse op på det, en forstår ikke hvordan man opskriver beviser endu, men vil vildt gerne vide hvordan man gøre det med sådan en.

Jeg ville skrive de 3 udtryk op som du har i #1, adskilt af lighedtegn, en ad gangen og regne dem ud med definitionen af skalarprodukt af to vektorer (https://www.webmatematik.dk/lektioner/matematik-b/vektorer-i-2d/skalarprodukt).

Det skulle gerne vise at de 3 udtryk giver det samme.

F.eks.:

Har checket den hjemmeside, men ikke særlig brugbar når der er tale om den formel jeg har tænkt mig at lave bvis for

   
            *     =       **    =       ***
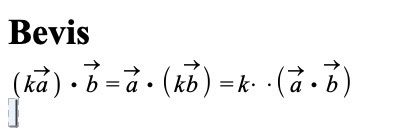
Du har beviset stående sidste linje # 12. Skriver vi det helt ud, får det følgende udseende:
Lad k være et vilkårligt reelt tal, vektor a koordinaterne (a₁ ; a₂) og vektor b koordinaterne (b₁ ; b₂).
Da har vi:
                                   b = (b₁ ; b₂)     kb = (kb₁ ; kb₂)          a • b = (a₁b₁ + a₂b₂)                                    
k                                                                                                       ***
a = (a₁ ; a₂)                                                  **
ka = (ka₁ ; ka₂)                    *

Produktet  * ,  **  og  ***   giver samme resultat. Da er sætningen vist.