Matematik
Differentialregning
Hej er der nogen derude som har mulighed for at forklare mig, hvordan man tackler denne her opgave. (vedhæftet) .
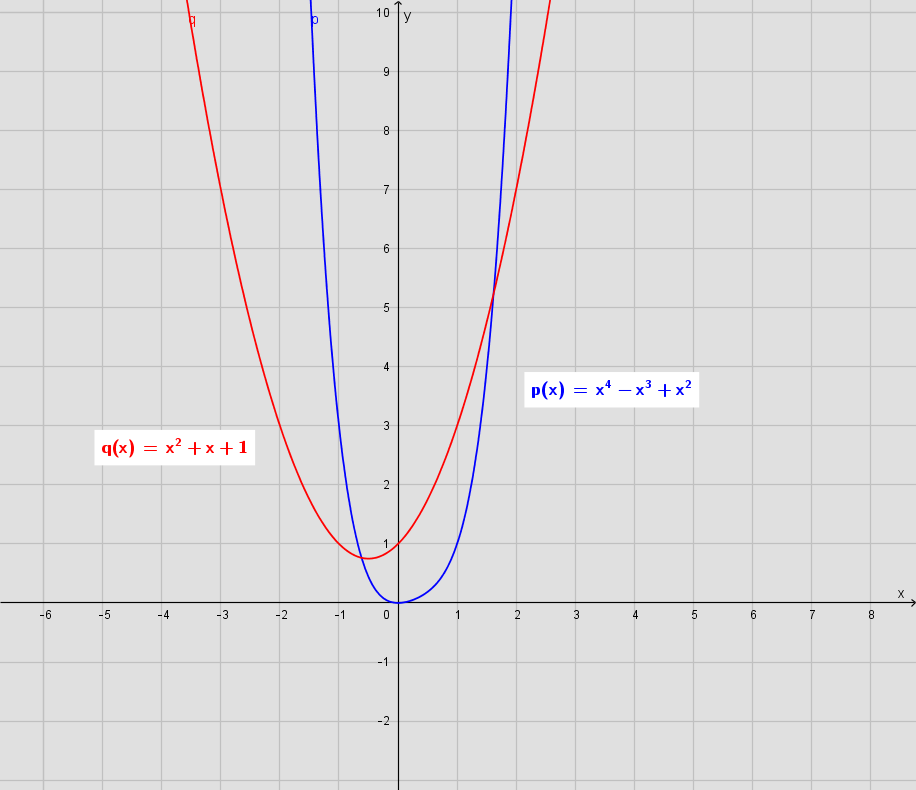
f(x)= x^4 -x^3 +x^2
og den har monotoniforholdet:
aftagende og så voksende.
Jeg ville bare høre, om hvordan man egentlig angiver en andengradsfunktion, der har samme monotoniforhold. Er der en konkret måde?
Svar #1
18. oktober 2023 af MentorMath
Hej,
Vi kan bestemme en regneforskrift for en andengradsfunktion, der har samme monotoniforhold, ved kigge på betydningen af konstanten a for en andengradsfunktion på formen y = ax2 + bx + c.
Vi kan opskrive udtrykket for en funktion g, der har samme monotoniforhold som f, ved at lade g være en andengradsfunktion, hvis a-værdi er positiv (grenene peger opad - aftagende og så voksende), og som har toppunkt for den x-værdi, hvori funktionen f har ekstremum.
Håber forklaringen giver mening?
Svar #2
18. oktober 2023 af peter lind
x4 + x3 + x2 = x2(x2 + x +) så polynomiet x2+x+1 har samme monotoniforhold som f
Svar #5
19. oktober 2023 af SuneChr
# 2 Læg mærke til, at koefficienten til x3 er negativ.
g(x) = x2 og f(x) har samme monotoniforhold og endda samme nulpunkt. Kan det blive bedre?
________________
x2 er også et polynomium, som alene består af leddet i højeste grad.
Man kunne, uofficielt, kalde det monomium, - men sig det ikke til nogen.
Svar #6
19. oktober 2023 af sofia877
Tusind tak for svar, I er virkelig kloge.
Jeg har bare et spørgsmål #5 . Hvordan kom du frem til det polynomium?
Svar #7
19. oktober 2023 af SuneChr
Ved at se på, og beregning af, det grafiske forløb for kurven til f ,
får man umiddelbart associationer, til en af de mest grundlæggende
kurver vi kender, nemlig parablen med forskriften g(x) = x2.
Vi kunne også bruge g(x) = ax2 for alle a > 0, men hvorfor ikke nøjes med
at sætte a = 1.
Svar #9
19. oktober 2023 af peter lind
#6
Jeg kom frem til det ved at se f(x) = x2*g(x) f og g er kontnuerte differentable
x2≥0 og kun 0 for x=0
Hvis g(x) vokser i et eller andet punkt må f(x) også vokse og omvendt hvis g(x) aftager må f(x) også aftager
det kan også skrives g(x+dx)-g(x) > 0 må det også gælde f(x)
Skriv et svar til: Differentialregning
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.