Matematik
hjælp med Opgave 3.14 i mat b
I den vilkårlige trekant ABC er [a] = 7,5 cm, [b] = 9,6 cm og [A=50^\circ] .
Vis, at der findes to trekanter med de givne størrelser.
Hvor lang skal siden [b] være, for at der netop ikke er to trekanter?
hvad gør jeg her
Svar #1
05. december 2023 af oppenede
Start med at tegne det af trekanten som du kan ud fra oplysningerne
Svar #2
05. december 2023 af ringstedLC
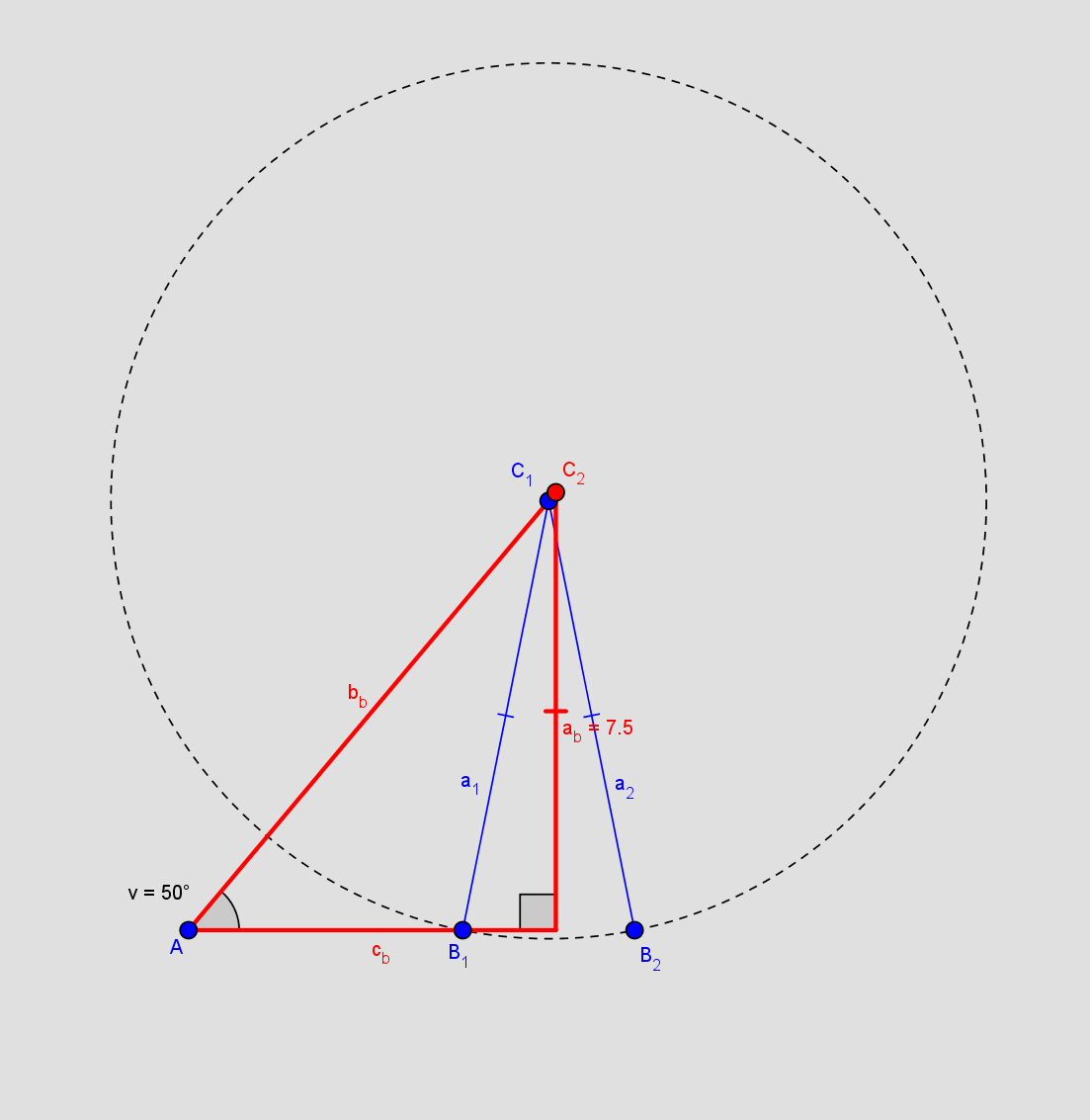
Med kun en trekant er de to blå sider sammenfaldende med den røde. Siden bb kan da beregnes med sinusrelationen for en retvinklet trekant.
Svar #3
05. december 2023 af SuneChr
Benyt den officielle terminologi for en trekants sider og vinkler.
Vi har ΔABC, a = 7,5 b = 9,6 A = 50º hvad betyder det, du har skrevet om A? Er A = 50º?
Vi har et af de fem trekantstilfælde, hvor en vinkel, dens modstående og en af dens hosliggende sider er givne.
Afsæt først b og dernæst A og forlæng siden, som er c. Med a i passeren og med nålen i C slå en bue
som gennemskærer to steder på c.
Skal vi bibeholde A og a og forandre b således, at der er en og kun en løsning, skal vi forlænge b
til b1 således at a ⊥ c.
Benyt sinusrelationen
hvor B = 90º
Skriv et svar til: hjælp med Opgave 3.14 i mat b
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.




