Matematik
Isolering af x i en opgave med en taperulle!
Hejsa!
Er der nogen som evt. har styr på isolering af x (i denne opgave n) i følgende opgave, som evt. kunne hjælpe mig?
50000 = π * 0,1 * n2 + 2 * π * 25 * n
Hele opgaven lyder:
I en model for en taperulle kan længden af tape på rullen L8n) som funktion af n af vinklinger af tape på rullen beskrives ved:
L(n) = π * d * n2 + 2 * π * r0 * n
L(n) = Længden af taperullen
n = Viklinger af tape på rullen
d = tykkelsen
r0 = radius af den tomme rulle.
For en bestemt rulle tape er tykkelsen d = 0,1 mm, mens radius af den tomme rulle r0 = 25.
a) Bestem tallet af vinklinger i taperullen, når længden af tape er 50000 mm.
50000 = π * 0,1 * n2 + 2 * π * 25 * n
Skriver jeg det i et CAS-værktøj så får jeg to løsninger på x. Jeg får -705,569 ELLER 225,569.
Hvad skal jeg bruge de to resultater til? Det kan vel kun være det positive tal som er løsningen på opgaven... eller hvad?
Kan man tegne en graf over dette, og i tilfælde af at man kan... Hvordan skal dette så gøres?
- På forhånd tak!
Svar #2
18. august 2014 af Hippocampus (Slettet)
Det ligner en opgave med hjælpemidler, som du passende kan løse med et CAS-værktøj.
Svar #4
18. august 2014 af Eksperimentalfysikeren
#3: Ligningen i #1 er korrekt. Det er en korrekt omskrivning af den oprindelige ligning.
#0: Det er, som du nævner, kun den positive rod, der er løsning til problemet.
Svar #5
18. august 2014 af Andersen11 (Slettet)
Der er med meget stor sandsynlighed tale om Opg. 11 i dette eksamenssæt
http://www.uvm.dk/~/media/UVM/Filer/Udd/Gym/PDF13/131206%20MatA-stx-06122013.ashx
Længden af tape på rullen som funktion af antallet n af viklinger tape på rullen er givet ved
L(n) = π·d·n2 + 2·π·r0·n
hvor d er tykkelsen af tapen og r0 er radius af den tomme rulle. I spm b) skal man bestemme n for en rulle tape med d = 0,1 mm , r0 = 25 mm, hvor den samlede længde af tapen er L = 50000 mm , og man skal der løse ligningen
50000 = 0,1·π·n2 + 50·π·n
som en 2.-gradsligning i n, hvor man som nævnt i #4 begrænser sig til den positive rod.
Svar #6
18. august 2014 af SuneChr
Formlen i # 0 for den udrullede tapes længde er ikke korrekt.
Man kan hurtigt se det ved at prøve at indsætte n = 1, nemlig den første omvikling af den tomme spole.
Iflg. formlen skulle tapen ha' en længde på ........................................................... π·(d + 2·r0)
Måles i forhold til tapens underside, med klisteret på, fås omkredsen af første vinding 2·π·r0 ,
måles i forhold til tapens overside fås omkredsen af første vinding ...................... 2·π·(d + r0)
Ligningen, m.h.t. tapens underside, er da som anført i # 1 med den korrektion som nævnt i # 3.
Det skal så understreges, at forskellen i den udrullede tape er godt og vel 23 cm, når man tager hensyn til, om det er over- eller undersiden af tapen, der ligger til grund.
Svar #7
18. august 2014 af Andersen11 (Slettet)
Formlen for L(n) i #5 er korrekt med god nøjagtighed, hvis vi bruger midten af tapens tykkelse som måler for beregningen af tapens længde.
Den første vinding vil have en gennemsnitlig radius på r0 + (d/2) med en længde 2π·(r0 + (d/2)) .
Vinding nr 2 vil have en radius på r0 + (d/2) + d, med en længde 2π·(r0 + (d/2) + d) .
Vinding nr k vil have en radius på r0 + (d/2) + (k-1)·d med en længde 2π·(r0 + (d/2) + (k-1)·d) .
Den samlede længde af n vindinger er da
L(n) = ∑nk=1 2π·(r0 + (d/2) + (k-1)·d)
= n·2π·(r0 + (d/2)) + 2π·d·∑nk=1 (k-1)
= n·2π·(r0 + (d/2)) + 2π·d·(n-1)·n/2
= 2π·r0·n + π·d·n2 .
Svar #8
18. august 2014 af SuneChr
Med tapens underside: (slet " - λ = 0 " til sidst)
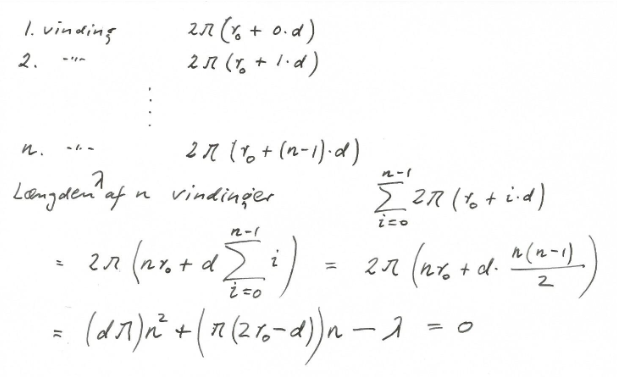
Svar #9
18. august 2014 af Andersen11 (Slettet)
Det er vel så ikke overraskende, at det i opgaven benyttede udtryk for L(n) netop er gennemsnittet af udtrykket, der fås ved at benytte tapens inderside:
Linderside(n) = 2π·r0·n - π·d·n + π·d·n2
og udtrykket, der fås ved at benytte tapens yderside:
Lyderside(n) = 2π·r0·n + π·d·n + π·d·n2 ,
dvs.
L(n) = (1/2)·(Linderside(n) + Lyderside(n)) = 2π·r0·n + π·d·n2 .
Skriv et svar til: Isolering af x i en opgave med en taperulle!
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.






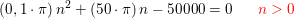 en andengradsligning i n
en andengradsligning i n