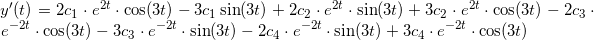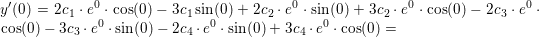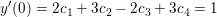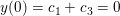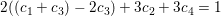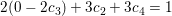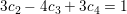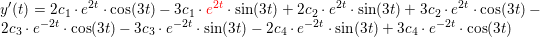Matematik

Partikulær løsning

26. august 2014 af lufthansa (Slettet) - Niveau: Universitet/Videregående

Jeg har følgende

y(t) = c₁e^2t*cos(3t)+c₂e^2tsin(3t)+c₃e^-2tcos(3t)+c₄e^-2tsin(3t)

Så skal jeg finde en partikulær løsning til y(t) for y(0) = 0 og y'(0) = 1

Jeg kender allerede resultatet men kan ikke finde ud af hvordan det er fremkommet

Det skal give y(t) = 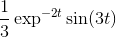$\frac{1}{3}\exp ^{-2t}\sin(3t)$

Nogen som kan forklarer mig hvordan jeg kommer frem til dette resultat ?

Brugbart svar (0)

Svar #1
26. august 2014 af peter lind

Find y'(t)

Løs ligningerne

y(0)=0

y'(0) = 1

Du har 4 integrationskonstanter, så der må være flere oplysninger til at bestemme c₁,c₂,c₃,c₄

Svar #2
26. august 2014 af lufthansa (Slettet)

Spørgsmålet lyder

(ii) Vis at differentialligningen har netop ´en partikulær løsning y = f(t)

for hvilken

f(0) = 0, f′(0) = 1, og f(t) → 0 for t → ∞.

Og diff ligningen som har den fuldstændige løsning som beskrevet som y(t) ovenover er

d⁴y/dt⁴+10*d²y/dt²+169y = 0

Det er alt hvad jeg har og så svaret altså.

Brugbart svar (0)

Svar #3
26. august 2014 af peter lind

f(t) -> 0 holder kun for e^-2t så c₁=c₂=0

Brugbart svar (0)

Svar #4
26. august 2014 af mathon

$\small \! \! \! \! \! \! \! \! \! \! y{}'(t)=2c_1\cdot e^{2t}\cdot \cos(3t)-3c_1\sin(3t)+2c_2\cdot e^{2t}\cdot \sin(3t)+3c_2\cdot e^{2t}\cdot \cos(3t)-2c_3\cdot e^{-2t}\cdot \cos(3t)-3c_3\cdot e^{-2t}\cdot \sin(3t)-2c_4\cdot e^{-2t}\cdot \sin(3t)+3c_4\cdot e^{-2t}\cdot \cos(3t)$

$\small \small \! \! \! \! \! \! \! \! \! \! y{}'(0)=2c_1\cdot e^{ 0}\cdot \cos(0)-3c_1\sin(0)+2c_2\cdot e^{0}\cdot \sin(0)+3c_2\cdot e^{0}\cdot \cos(0)-2c_3\cdot e^{0}\cdot \cos(0)-3c_3\cdot e^{0}\cdot \sin(0)-2c_4\cdot e^{0}\cdot \sin(0)+3c_4\cdot e^{0}\cdot \cos(0)=$

$\small \small y{}'(0)=2c_1+3c_2-2c_3+3c_4=1$

og
$\small y(0)=c_1+c_3=0$

Brugbart svar (0)

Svar #5
26. august 2014 af mathon

hvoraf:

$\small \small \small \small 2((c_1+c_3)-2c_3)+3c_2+3c_4=1$

$\small \small \small \small \small 2(0-2c_3)+3c_2+3c_4=1$

$\small 3c_2-4c_3+3c_4=1$

Brugbart svar (0)

Svar #6
26. august 2014 af mathon

korrektion
$\small \small \! \! \! \! \! \! \! \! \! \! y{}'(t)=2c_1\cdot e^{2t}\cdot \cos(3t)-3c_1\cdot {\color{Red} e^{2t}}\cdot \sin(3t)+2c_2\cdot e^{2t}\cdot \sin(3t)+3c_2\cdot e^{2t}\cdot \cos(3t)-2c_3\cdot e^{-2t}\cdot \cos(3t)-3c_3\cdot e^{-2t}\cdot \sin(3t)-2c_4\cdot e^{-2t}\cdot \sin(3t)+3c_4\cdot e^{-2t}\cdot \cos(3t)$

hvilket ikke ændrer på udtrykket for y '(0)

Svar #7
26. august 2014 af lufthansa (Slettet)

Tak for hjælpen indtil nu. Men jeg har stadig ikke forstået hvordan jeg kommer frem til resultatet !

Jeg forstår metoden indtil udtrykket for y'(0) samt svar #5.

Men det sidste ?

Brugbart svar (1)

Svar #8
26. august 2014 af peter lind

Se #3 c₁= c₂ = 0

Indsætter du det i den sidste ligning i #4 får du c₃=0. Indsætter du så i den næstsidste ligning får du en ligning til bestemmelse af c₄

Brugbart svar (1)

Svar #9
26. august 2014 af Andersen11 (Slettet)

Det er oplyst, at differentialligningen har den generelle løsning givet i #0:

y(t) = c₁e^2t·cos(3t) + c₂e^2t·sin(3t) + c₃e^-2t·cos(3t) + c₄e^-2t·sin(3t)

= (c₁e^2t+c₃e^-2t)·cos(3t) + (c₂e^2t+c₄e^-2t)·sin(3t) ,

der har differentialkvotienten

y '(t) = (2c₁e^2t-2c₃e^-2t+3c₂e^2t+3c₄e^-2t)·cos(3t) + (-3c₁e^2t-3c₃e^-2t+2c₂e^2t-2c₄e^-2t)·sin(3t) .

Hvis en løsning skal opfylde y(0) = 0 og y '(0) = 1, indsætter man t = 0 i udtrykkene for y(t) og y '(t) og finder

y(0) = c₁ + c₃ = 0

y '(0) = 2c₁ - 2c₃ + 3c₂ + 3c₄ = 1 .

Hvis der yderligere skal gælde, at y(t) → 0 for t → ∞ , må der også gælde, at c₁ = 0 og c₂ = 0. Dermed kan c₃ og c₄ bestemmes entydigt, dvs. der er netop én partikulærløsning, der opfylder de givne betingelser.

Svar #10
26. august 2014 af lufthansa (Slettet)

Svar #8 til Peter

Tror du at du kunne forklare mig hvorfor f(t) -> 0 holder kun for e-2t så c1=c2=0 fra dit svar #3 ?

Brugbart svar (1)

Svar #11
26. august 2014 af Andersen11 (Slettet)

#10

En funktion af formen c·e^kt , hvor |c|>0 og k > 0 , går mod ±∞ for t → 0 . Da cos(3t) og sin(3t) er begrænsede, men ikke går mod 0 for t → ∞, vil en funktion af formen (c₁·cos(3t) + c₂·sin(3t))·e^2t kun gå mod 0, hvis både c₁ og c₂ er lig med 0.

Svar #12
26. august 2014 af lufthansa (Slettet)

#11 tusind tak

Skriv et svar til: Partikulær løsning

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.