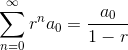Induktion - vis uligheden

Løs ulighederne 2-½x ≤ 5/3 og 2-½x ≥ 2/3

#1, Så får jeg at a_n ≥ 2/3 og a_n ≤ 8/3.

Det er vel ikke det jeg skulle få. 

Dermed har du vist at   2/3 ≤ 2-½x ≤ 5/3  <=> 2/3 ≤ x ≤ 8/3

Da der gælder [2/3, 5/3]⊂ [2/3;8/3]  vil a_n-1 ∈ [2/3; 5/3]  => 2-½a_n-1= a_n ∈ [2/3; 5/3]

#3, Jeg kan se hvad du mener. Tak skal du have!

Du ved vel ikke hvordan man kan finde konvergensradius ud fra dette, vel?
Lige umiddelbart ville jeg mene, at det er  |r| < 1, da det er en geometrisk række. Men der står i opgaven, at jeg skal benytte hvad jeg har fundet frem til, til at bestemme konvergensradius.. 

Du har at 2*xⁿ/3 er en minorant række og 5*xⁿ/3 og de begge har konvergensradius 1 må det samme gælde for den givne række

Skulle det ikke være 2/3 ≤ a_n ≤ 5/3 ⇔ 2/3 ≤ a_{n - 1} ≤ 8/3?

Hvis dette er gjort, skulle man ikke vise 2/3 ≤ a_n og a_n ≤ 5/3 vha. induktionen hver for sig?

#5, Er det en skrivemåde du har fra summen for en geometrisk række? 

#6 Det gælder også, men du har faktisk vist den noget skrappere begrænsning for a_n

#7 jo

#8, men så er konvergensradius vel givet ved |r| < 1 og ikke |r| = 1. 

Nej. for ethvert endelig n og x ≥0 gælder

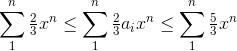
Da den højre sum er konvergent for x ∈[0;1] og midtersummen er monoton voksende er midtersumme konvergent i intervallet. Da venstre side er divergent for x > 1 må midtersummen også være det. altså er midtersummen konvergent for x ∈[0,1]

#10, Er udtrykket ikke givet ved 

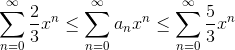
Så vidt jeg kan se er både højre og venstre side konvergent for  x ∈[0;1], og derfor må midtersummen også være det. 

Du har ret i at de 2/3 i midtersummen er forkert. og ja du kan af dette slutte at midtersummen er konvergent

#12, dvs. at konvergensradius, r = 1, ikke sandt? 

Af #8 kan du slutte at konvergensradius er mindst 1. For at bevise at konvergensradius ikke er større end 1 skal du vise at rækken er divergent for x > 1. Dette er gjort i #10

Tak for hjælpen Peter Lind :)

rettelse til det foregående. Ingen af rækkerne er konvergent for x = 1. De lukkede intervaller skal altså laves om til halvåbne