Matematik

Integral

12. juni 2015 af Niko83 (Slettet) - Niveau: Universitet/Videregående

Hej derude.
Jeg har en opgave, der lyder:
Lad B være.

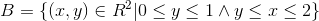
$B=\{(x,y)\in R^2|0 \leq y\leq1 \wedge y\leq x \leq 2\}$

1. Beregn planintegralet 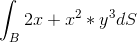$\int _B 2x +x^2*y^3dS$

Lad nu 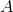være;
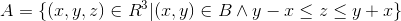
$A=\{(x,y,z)\in R^3|(x,y)\in B \wedge y-x \le z \le y+x\}$

2. Beregn rumintegralet 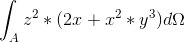$\int _A z^2*(2x+x^2*y^3)d\Omega$

Jeg har tænkt i (1) at jeg kunne regne planintegralet på følgende måde.

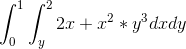$\int_{0}^{1}\int_{y}^{2}2x+x^2*y^3 dxdy$ (jeg ved ikke hvis det er rigtigt).

Jeg har også tænkt i (2) at jeg kunne beregne rumintegralet på følgende måde.

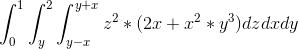$\int_{0}^{1}\int_{y}^{2}\int_{y-x}^{y+x} z^2* (2x+x^2*y^3)dzdxdy$ .

Vil nogen derude fortælle hvis opgaven er rigtigt eller forkert?.
Jeg håber, at høre af nogen derude.

Brugbart svar (0)

Svar #1
12. juni 2015 af Toonwire

Du har den rigtige idé, men du mangler lige en gennemgående væsentlig ting; Jacobifunktionen.

Der gælder at man for en parametriseret flade 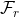kan udregne dets planintegrale på følgende vis:

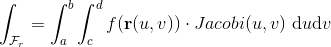
$\int_{\mathcal{F}_r}=\int_a^b\int_c^d{f(\mathbf{r}(u,v))}\cdot Jacobi(u,v)~\text{d} u\text{d} v$

Og ligeledes for rumintegralet:

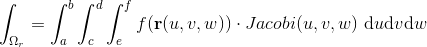
$\int_{\Omega_r}=\int_a^b\int_c^d\int_e^f{f(\mathbf{r}(u,v,w))}\cdot Jacobi(u,v,w)~\text{d} u\text{d} v \text{d}w$

Vær opmærksom på hvordan Jacobifunktionen udregnes i de forskellige tilfælde!

For en plan udregnes Jacobifunktionen ved længden af krydsproduktet mellem de to afledte parametriseringsvektorer.
I rummet findes Jacobifunktion ved numerisk determinantafgørelse blandt de afledte.

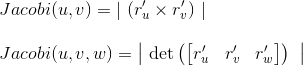
$\\Jacobi(u,v)=\left|~(r'_u \times r'_v)~\right|\\\\ Jacobi(u,v,w)=\left|~\text{det}\left(\begin{bmatrix} r'_u&r'_v &r'_w \\ \end{bmatrix}\right)~\right|$

Skriv et svar til: Integral

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.