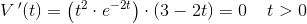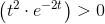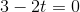hjælp !

24. oktober 2015 af annie4567 (Slettet) - Niveau: A-niveau

Jeg har opgaven:

En rottes vægt: V(t) ( målt i kg) som funktion af dens alder t (målt i år) beskrives ved modellen

V(t)= t^ae^-2t

hvor a er positiv parameter.

(b)

Lad a=3. Det oplyses, at der gælder:

V'(t)=t²(3-2t)e^-2t

Bestem den alder, hvor en rotte når sin maksimalvægt.

Jeg er med på man sætter V'(t) = 0 og isolere t, men når t indtræffer flere gange i funktionen, hvordan isoleres den så?

Brugbart svar (0)

Svar #1
24. oktober 2015 af StoreNord

Kun det ene sted er vægten positiv.

Brugbart svar (0)

Svar #2
24. oktober 2015 af mathon

$V{\, }'(t)=\left ( t^2\cdot e^{-2t} \right )\cdot (3-2t)=0\; \; \; \; t>0$

$\left ( t^2\cdot e^{-2t} \right )>0$
hvoraf
3-2t=0

Brugbart svar (0)

Svar #3
24. oktober 2015 af StoreNord

f' er godt nok 0 tre stedet, men kun det ene sted vejer rotten noget. :)

Se her:En rottes vægt

Vedhæftet fil:En rottes vægt.png

Svar #4
24. oktober 2015 af annie4567 (Slettet)

Ahh så den har maksimum i t=1,5. Dvs. at rotten når sin maksimalvægt i den alder :)

tak for hjælpen

Brugbart svar (0)

Svar #5
24. oktober 2015 af StoreNord

170 gram!

Det må da vist være en dværgrotte?

Skriv et svar til: hjælp !

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.