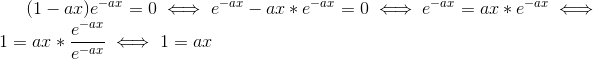bestemme maksimum for funktion

Benyt 0-reglen.
e^-ax > 0
Kig derfor på faktoren foran.

Hvis (1-ax)e^-ax=0,

så må enten være 0, eller e^-ax være 0.

Og jeg ved godt, hvad for een der aldrig kan være 0.     :)

hm skal jeg så dele leddene op sådan

1-ax =0

og 

e^-ax =0

eller Jeg er ikke helt med på hvordan jeg kan vise det ?

Hmm, de bruger 0-reglen, altså A*X=0 <-> A=0 eller X=0, da e^-ax altid er større end 0 (du kan jo forsøge at sætte nogle værdier ind) ved du at hvis (1-ax)e^-ax=0 bliver1-ax nød til at være 0. Ergo kan du finde løsningen ved løse 1-ax=0 :)

Alternativt kan du også se det som

#2

Hvis (1-ax)e^-ax=0,

så må enten være 0, eller e^-ax være 0.

Og jeg ved godt, hvad for een der aldrig kan være 0.     :)

Lige en rettelse: (undskyld)

Hvis         f'(x)=(1-ax)e^-ax=0,

så må enten parentesen være 0, eller e^-ax må være 0.

Og jeg ved godt, hvad for een der aldrig kan være 0.     :)

Tak for hjælpen ! og kan man altid anvende nulreglen i situationer som denne ? hvor x er flere steder :)?

I dit spørgsmål havde du et produkt på venstre side.

                  f'(x)=(1-ax)*e^-ax=0          Et produkt et nul, hvis bare een af faktorerne er nul.

men hvis det så sådan her ud (som er det samme):

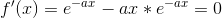                      Var det ikke til at overskue.

Og her:      f'(x)=(1-ax)+e-ax=0  kan vi ikke bruge nulreglen, men nu er jeg også ude på et sidespor.  :)