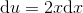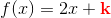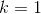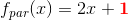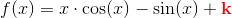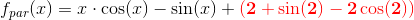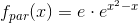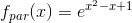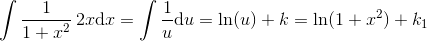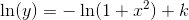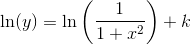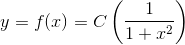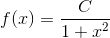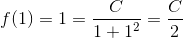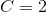Matematik
Bestem den fuldstændige løsningsmængde til differentialligningerne (integrer gerne de fire sidste delopgaver i de fire første):
Bestem den fuldstændige løsningsmængde til differentiallligningerne (integrer gerne de fire sidste delopgaver i de fire første):
De 8 opgaver er vedlagt:
Mange tak på forhånd.
Svar #9
16. februar 2016 af Hansen5000 (Slettet)
Kan vi lige tage opgave:
e)
f)
g)
h)
det forstår jeg ikke helt.
Svar #10
16. februar 2016 af Soeffi
Opgaven har nogle sproglige unøjagtigheder. For det første blander man f(x) og y. f(x) og y er det samme. For det andet tales der om at integrere. Det skal nok forstås som at inddrage eller medtage - ikke at integrere i snæver matematisk forstand.
I spørgsmål a) - d) får du nogle fuldstændige løsninger, hvor der indgår en konstant i hver. Det er disse konstanter, der skal findes i e) - g). Til hver værdi af konstanterne hører en partikulær løsning til hver af differentialligningerne.
Skriv et svar til: Bestem den fuldstændige løsningsmængde til differentialligningerne (integrer gerne de fire sidste delopgaver i de fire første):
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.









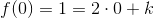
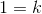
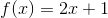
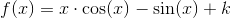
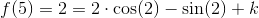
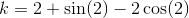
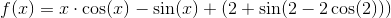
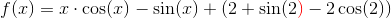
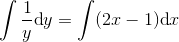
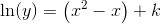
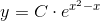


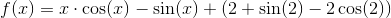
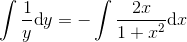
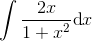 benytter substitutionen
benytter substitutionen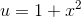 og dermed
og dermed