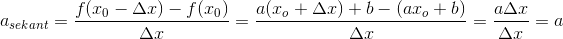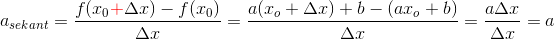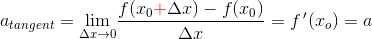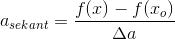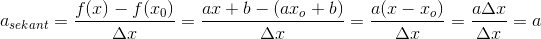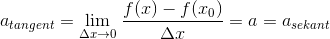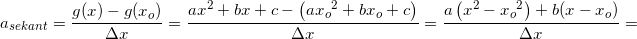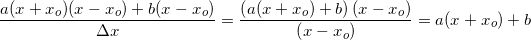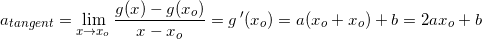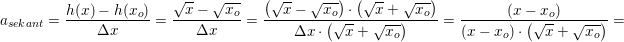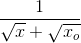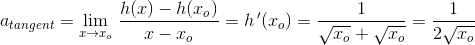Matematik

Tretrinsreglen

16. juni 2016 af Sara2303 (Slettet) - Niveau: B-niveau

Hej med Jer,
Jeg skal til min mundtlige eksamen forberede nogle eksempler på polynomier, som jeg skal løse vha. tretrinsreglen.

Jeg ved, at jeg skal bruge formlen 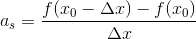$a_{s} = \frac{f(x_0 -\Delta x)-f(x_0)}{\Delta x}$

Men kan i komme med et par eksempler, andre end f(x)=x, f(x)=x^2 og f(x)=x^3? :) Jeg er nemlig lidt i tvivl om hvilke funktioner man kan indsætte. Jeg ved godt, at der skal være en potens, men kunne godt tænke mig nogle flere eksempler :)

Brugbart svar (0)

Svar #1
16. juni 2016 af peter lind

Du kan jo prøve med 3x²+2x+3 eller evt mere generelt a*x²+b*x+c

Brugbart svar (0)

Svar #2
16. juni 2016 af MatHFlærer

Prøv:
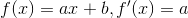
f(x)=ax+b, f'(x)=a

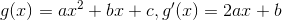
g(x)=ax^2+bx+c, g'(x)=2ax+b

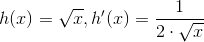
$h(x)=\sqrt{x}, h'(x)=\frac{1}{2\cdot\sqrt{x}}$

Disse er rigtig gode at kunne anvende til den mundtlige eksamen. Jeg bad mine kursister på B-niveau om at udlede mindst en af disse tre ovenstående. Held og lykke.

Brugbart svar (1)

Svar #3
16. juni 2016 af mathon

se evt.
https://www.studieportalen.dk/forums/thread.aspx?id=1688896 2) og 3)

Brugbart svar (0)

Svar #4
17. juni 2016 af MatHFlærer

Meget flot, #3. Det sådan man skal gøre.

Svar #5
17. juni 2016 af Sara2303 (Slettet)

Mange tak for svarene :) Men jeg er virkelig i tvivl om hvordan man sætter ind i formlen.

Hvis jeg nu tager eksempel 1 fra #2, f(x)=ax+b. Jeg forstår vitterligt ikke, hvad og hvordan disse informationer skal indføres i tretrinsreglen? :)

Og tak for hjælpen ellers Mathon #3, men jeg kan desværre ikke åbne filerne i den linkede tråd. (eller jo, men kan ikke se udregningerne, blot ''trin 1, trin 2, trin 3'' med rød tekst)

Brugbart svar (1)

Svar #6
17. juni 2016 af mathon

$a_{sekant} = \frac{f(x_0 -\Delta x)-f(x_0)}{\Delta x}=\frac{a(x_o+\Delta x)+b-\left ( ax_o+b \right )}{\Delta x}=\frac{a\Delta x}{\Delta x}=a$

$a_{tangent} =\underset{\Delta x \to 0}{\lim} \frac{f(x_0 -\Delta x)-f(x_0)}{\Delta x}=f{\, }'(x_o)=a$

Brugbart svar (0)

Svar #7
17. juni 2016 af mathon

tegnkorrektion

$a_{sekant} = \frac{f(x_0 {\color{Red} +}\Delta x)-f(x_0)}{\Delta x}=\frac{a(x_o+\Delta x)+b-\left ( ax_o+b \right )}{\Delta x}=\frac{a\Delta x}{\Delta x}=a$

$a_{tangent} =\underset{\Delta x \to 0}{\lim} \frac{f(x_0 {\color{Red} +}\Delta x)-f(x_0)}{\Delta x}=f{\, }'(x_o)=a$

Svar #8
17. juni 2016 af Sara2303 (Slettet)

Okay tusind tak, det hjalp meget lige at få det stillet op :) hvis jeg nu prøver med andengradspolynomiet, er dette så et korrekt udgangspunkt?:

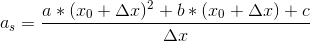
$a_s = \frac{a*(x_0+\Delta x)^2 + b* (x_0+ \Delta x )+c}{\Delta x}$

Svar #9
17. juni 2016 af Sara2303 (Slettet)

Men lige et spørgsmål mere til ax+b - er det overhovedet et polynomie? Kræver det ikke, at der er en potens før det kan kaldes et polynomie?

Brugbart svar (0)

Svar #10
17. juni 2016 af mathon

men måske mener du
$a_{sekant}=\frac{f(x)-f(x_o)}{\Delta a}$

så
$a_{sekant} = \frac{f(x)-f(x_0)}{\Delta x}=\frac{ax+b-\left ( ax_o+b \right )}{\Delta x}=\frac{a(x-x_o)}{\Delta x}=\frac{a\Delta x}{\Delta x}=a$

$a_{tangent}=\underset{\Delta x \to 0}{ \lim}\; \frac{f(x)-f(x_0)}{\Delta x}=a=a_{sekant}$

Brugbart svar (0)

Svar #11
17. juni 2016 af MatHFlærer

#9 f(x)=ax+b er et førstegradspolynomium, idet x er opløftet i første potens. Vi skriver bare aldrig tallet.

Brugbart svar (1)

Svar #12
17. juni 2016 af mathon

$\small a_{sekant} = \frac{g(x)-g(x_o)}{\Delta x}=\frac{ax^2+bx+c-\left ( a{x_o}^2+bx_o+c \right )}{\Delta x}=\frac{a\left ( x^2-{x_o}^2 \right )+b(x-x_o)}{\Delta x}=$

$\small \frac{a(x+{x_o})(x-{x_o})+b(x-x_o)}{\Delta x}=\frac{\left (a(x+x_o)+b \right )(x-x_o)}{\left (x-x_o \right )}=a(x+x_o)+b$

$\small \small a_{tangent} =\underset{x \to x_o}{ \lim}\, \frac{g(x)-g(x_o)}{x-x_o}=g{\, }'(x_o)=a(x_o+x_o)+b=2ax_o+b$

Brugbart svar (1)

Svar #13
17. juni 2016 af mathon

$\small a_{sekant} = \frac{h(x)-h(x_o)}{\Delta x}=\frac{\sqrt{x}-\sqrt{x_o}}{\Delta x}=\frac{\left (\sqrt{x}-\sqrt{x_o} \right )\cdot \left (\sqrt{x}+\sqrt{x_o} \right )}{\Delta x\cdot \left (\sqrt{x}+\sqrt{x_o} \right )}=\frac{\left ( x-x_o \right )}{\left ( x-x_o \right )\cdot \left ( \sqrt{x}+\sqrt{x_o} \right )}=$

$\frac{1}{ \sqrt{x}+\sqrt{x_o} }$

$a_{tangent} = \underset{x \to x_o}{\lim} \; \frac{h(x)-h(x_o)}{ x-x_o}=h{\, }'(x_o)=\frac{1}{\sqrt{x_o}+\sqrt{x_o}}=\frac{1}{2\sqrt{x_o}}$

Skriv et svar til: Tretrinsreglen

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.