Matematik

Determinent

21. november 2017 af Haaaaaaa - Niveau: B-niveau

Jeg har det svært med at udregne den opgave, håber der nogen gerne vil hjælpe til det

Vedhæftet fil: DETERMINANT .docx

Brugbart svar (0)

Svar #1
21. november 2017 af StoreNord

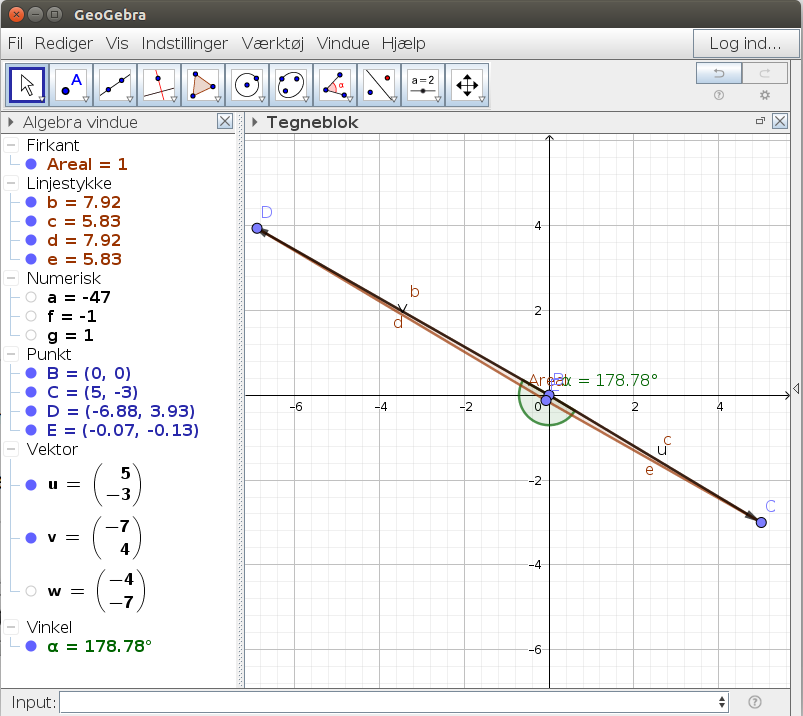
Arealet er: Den ene vektor prikket med den anden vektors tværvektor.

Brugbart svar (0)

Svar #2
21. november 2017 af StoreNord

I en anden bog læser jeg nu, at det skal være kryds-produktet.
Det er nok dèrfor der i 1984 kom et gult tillæg til den tynde blå formelsamling. :)

Brugbart svar (0)

Svar #3
21. november 2017 af peter lind

Hvis det er 2. dimensionale vektorer er #1 rigtig. Hvis det er 3 dimensionale vektorer er den numeriske værdi af krydspoduktet arealet som vektorerne udspænder. Krydsproduktet findes ikke for 2. dimensionale vektorer

Brugbart svar (0)

Svar #4
21. november 2017 af StoreNord

Tak

Svar #5
21. november 2017 af Haaaaaaa

5*4-(-3)*(-7)=20-(21)=41

9*10-12*(-7)=90-84 =6

kan det vær rigtig udregningen

Brugbart svar (0)

Svar #6
21. november 2017 af StoreNord

5*(-4)-(-3)*(-7)=-20-(21)=41 Det fik jeg også. Men jeg er nu ikke særligt sikker.

Brugbart svar (0)

Svar #7
21. november 2017 af StoreNord

Skærmbillede fra 2017-11-21 22-17-33.png

Vedhæftet fil:Skærmbillede fra 2017-11-21 22-17-33.png

Brugbart svar (0)

Svar #8
22. november 2017 af mathon

1)
$\small \small A_{par}=\begin{Vmatrix} 5 &-7 \\ -3& 4 \end{Vmatrix}=\left | 5\cdot 4-(-3)\cdot (-7) \right |=\left | 20-21 \right |=1$

Brugbart svar (0)

Svar #9
22. november 2017 af mathon

2)
$\small A_{par}=\begin{Vmatrix} 9 &-7 \\ 12& 10 \end{Vmatrix}=\left | 9\cdot 10-12\cdot (-7) \right |=\left | 90+84 \right |=174$

Brugbart svar (0)

Svar #10
22. november 2017 af mathon

3)
$\small \overrightarrow{AB}=\begin{pmatrix} 0-(-2)\\ 9-(-1) \end{pmatrix}=\begin{pmatrix} 2\\10 \end{pmatrix}$ $\small \overrightarrow{AC}=\begin{pmatrix} 4-(-2)\\ 3-(-1) \end{pmatrix}=\begin{pmatrix} 6\\4 \end{pmatrix}$

$\small T_{\Delta ABC}=\tfrac{1}{2}\cdot \left | det\left ( \overrightarrow{AB},\overrightarrow{AC} \right ) \right |=\tfrac{1}{2}\cdot \begin{Vmatrix} 2 &6 \\ 10 &4 \end{Vmatrix}=\tfrac{1}{2}\cdot \left | 2\cdot 4-10\cdot 6 \right |=\tfrac{1}{2}\cdot \left | -52 \right |=26$

Brugbart svar (0)

Svar #11
22. november 2017 af mathon

4)
$\small A_{par}=\begin{Vmatrix} q &2 \\ 6 &8 \end{Vmatrix}=24$

$\small \left | q\cdot 8-6\cdot 2 \right |=24$

$\small \left | 8q-12 \right |=24$

$\small 8q-12 =\mp 24$

$\small 8q =\mp 24+12=\left\{\begin{matrix} -12\\36 \end{matrix}\right.$

$\small q =\left\{\begin{matrix} -\frac{3}{2}\\\frac{9}{2} \end{matrix}\right.$

Svar #12
23. november 2017 af Haaaaaaa

tusinde tak for det

Brugbart svar (0)

Svar #13
23. november 2017 af MadsChristiansen89 (Slettet)

Følger lige med på sidelinjene...

Svar #14
23. november 2017 af Haaaaaaa

Hvad mener du, forstod ikke din meningen

Skriv et svar til: Determinent

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.