Matematik

Underrum af vektorrum

12. januar 2018 af JohnDoe1990 - Niveau: Universitet/Videregående

Ser nedenstående besvarelse fornuftig ud? Se vedhæftet opgaveformulering.

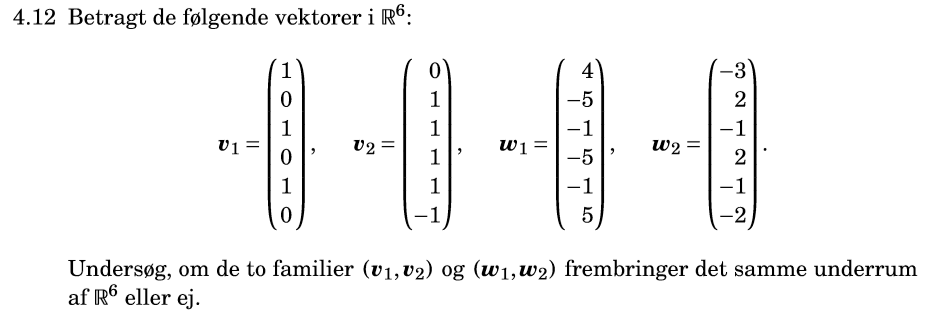
Det skal altså vises at for et hvert a i de frembragte underrum af R^6 findes skalarer x_1, x_2 i R, så a både er en lineær kombination af (v_1, v_2) og (w_1,w_2). Jeg har forsøgt at løse det på følgende måde:

Vi ser først at

$v_1x_1+v_2x_2 = \begin{pmatrix} x_1 \\ x_2 \\ x_1+x_2\\ x_2 \\ x_1+x_2\\ -x_2 \end{pmatrix}$

Det må også gælde at

$w_1x_1+w_2x_2 = \begin{pmatrix} 4x_1-3x_2 \\ -5x_1+2x_2\\ -x_1-x_2 \\ -5x_1+2x_2\\ -x_1-x_2 \\ 5x_1-2x_2 \end{pmatrix} = (4x_1-3x_2) \begin{pmatrix} 1\\ 0\\ 1\\ 0\\ 1\\ 0 \end{pmatrix} + (-5x_1+2x_2) \begin{pmatrix} 0\\ 1\\ 1\\ 1\\ 1\\ -1 \end{pmatrix}$

Da ser vi at:

$w_1x_1+w_2x_2 = v_1(4x_1-3x_2)+v_2(-5x_1+2x_2)$

Hvorfor enhver lineær kombination af v_1 og v_2 også kan udtrykkes som en lineær kombination af w_1 og w_2 og omvendt. Da må de frembringe det samme underrum.

Er der mon noget jeg har overset? Kan det gøres på en lettere måde evt.? Jeg er lidt i tvivl om, hvordan man normalt skriver overstående notationsmæssigt. Burde man bruge en anden notation for skalarerne x_1 og x_2 eks.?

Vedhæftet fil: SP.png

Svar #1
12. januar 2018 af JohnDoe1990

Brugbart svar (0)

Svar #2
12. januar 2018 af gtx1 (Slettet)

Man ser at begge basisvektorere i det ene underrum kan skrives som en linearkombination af basisvektorerne i det andet, og omvendt. Nemlig w₁=4v₁-5v₂ og w₂=-3v₁+2v₂ og ligeledes er 7v₁=-2w₁-5w₂ og 7v₂=-3w₁-4w₂. Dermed udspænder (v₁,v₂) og (w₁,w₂) det samme underrum.

Brugbart svar (0)

Svar #3
12. januar 2018 af fosfor

Svaret er ja, hvis der findes M som er 2x2 med det(M) ≠ 0.
$\left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \\ 1 & 1 \\ 0 & 1 \\ 1 & 1 \\ 0 & -1 \\ \end{array} \right)\cdot M=\left( \begin{array}{cc} 4 & -3 \\ -5 & 2 \\ -1 & -1 \\ -5 & 2 \\ -1 & -1 \\ 5 & -2 \\ \end{array} \right)$

Betragtes række 1 og 2 alene ses enhedsmatricen til venstre, hvorfor M nødvendigvis skal være
$M=\left( \begin{array}{cc} 4 & -3 \\ -5 & 2 \\ \end{array} \right)$
som opfylder det(M) ≠ 0. Tilstrækkelighed følger ved at regne ud at de resterende rækker også passer.

Skriv et svar til: Underrum af vektorrum

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.