Matematik

Ekstrema og Værdimængde

18. juli 2018 af Johan873 (Slettet) - Niveau: C-niveau

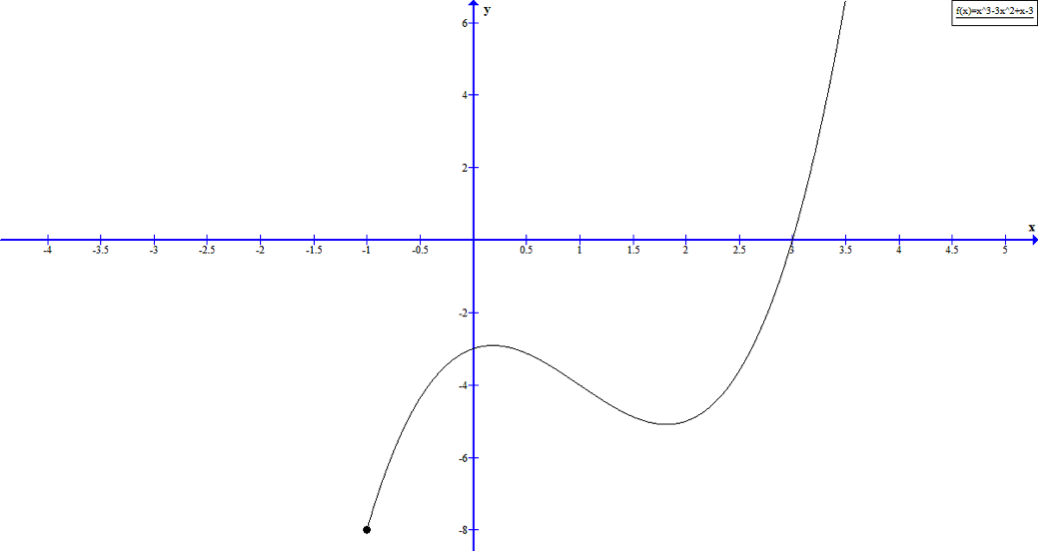
Er der nogen der kan bestemme funktionens ekstrema og værdimængde (Vm)

Vedhæftet fil: Ikke-navngivet.png

Brugbart svar (0)

Svar #1
18. juli 2018 af mathon

Brugbart svar (0)

Svar #2
18. juli 2018 af StoreNord

Ekstremer: y=-3 og y=-5
Værdimængde: [-8,∞[

Brugbart svar (0)

Svar #3
18. juli 2018 af mathon

$\small \textup{ekstrema bestemmes af:}$

$\small f{\, }'(x)=3x^2-6x+1=0$

$\small V\! m(f)=[-8;\infty]$

Brugbart svar (0)

Svar #4
18. juli 2018 af mathon

$\small \small 3x^2-6x+1=0$

$\small x=\left\{\begin{matrix} \frac{3-\sqrt{6}}{3}\\ \frac{3+\sqrt{6}}{3} \end{matrix}\right.$

$\small f(x)=\left\{\begin{matrix} -4+\frac{4\sqrt{6}}{9}\\ -4-\frac{4\sqrt{6}}{9} \end{matrix}\right.\approx \left\{\begin{matrix} -2.91\\-5.089 \end{matrix}\right.$

Brugbart svar (0)

Svar #5
18. juli 2018 af mathon

$\small \textup{fortegnsvariation}$
$\small \textup{for }f{\, }'(x):$    + 0 - 0 +
   -1__________0.18________1.82_________
$\small \textup{x:}$    $\small \textup{lok. max}$    $\small \textup{lok. min}$
$\small \textup{monotoni}$
$\small \textup{for f(x):}$     $\small \textup{voksende}$ $\small \textup{aftagende}$    $\small \textup{voksende}$

Brugbart svar (0)

Svar #6
18. juli 2018 af StoreNord

Skærmbillede fra 2018-07-18 16-34-38.png

Vedhæftet fil:Skærmbillede fra 2018-07-18 16-34-38.png

Brugbart svar (0)

Svar #7
18. juli 2018 af ringstedLC

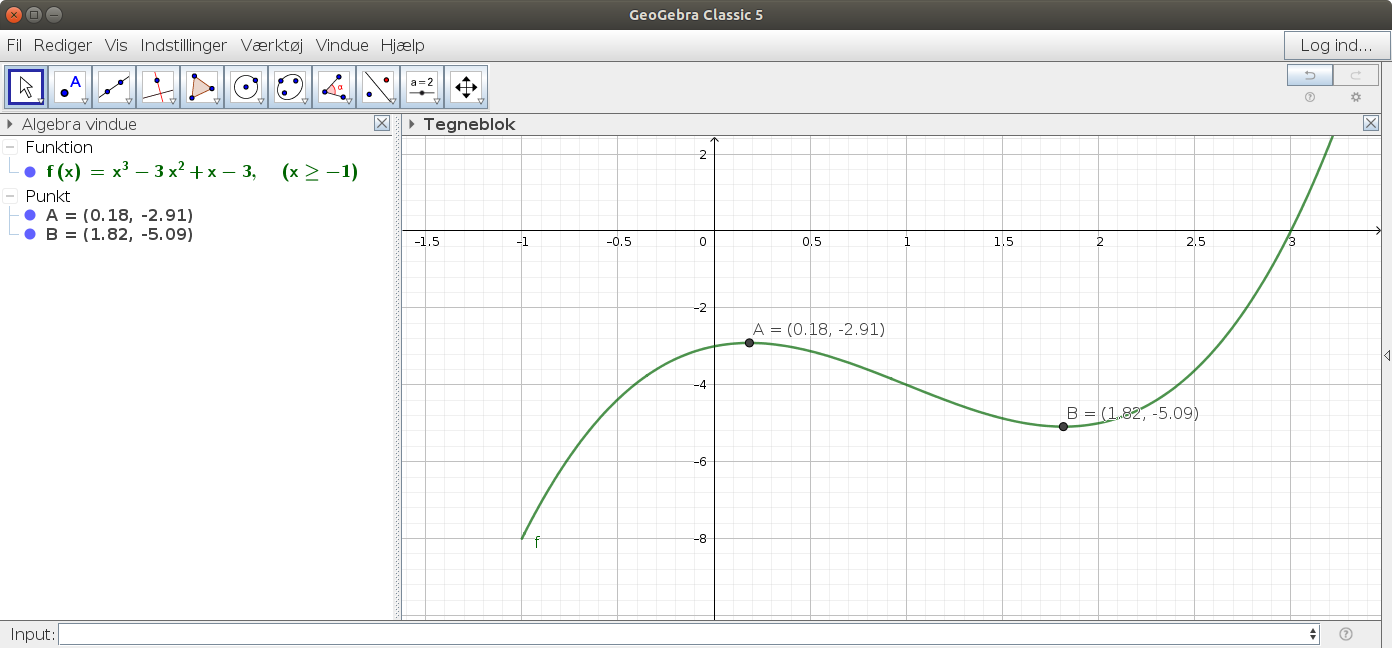
Ekstrema (minimum- og maksimumværdier): Det fremgår af grafen, at f har et globalt min. i (-1, 8).

Og et lokalt maks. og et lokalt min. som bestemmes ved at differentiere f:

$\begin{align*} {\color{Blue} f(x)}&\;{\color{Blue} =x^3-3x^2+x-3}\Downarrow\\ f'(x)&=3\cdot 1x^{3-1}-3\cdot 2x^{2-1}+1\cdot 1x^{1-1}-0\Downarrow\\ f'(x)&=3x^2-6x^1+1x^0\Downarrow\\ {\color{Red} f'(x)}&\;{\color{Red} =3x^2-6x+1} \end{align*}$

Differentialkvotienten sættes lig 0:

$\begin{align*} f'(x)&=0\Downarrow\\ 3x^2-6x+1&=0\\ x&=\frac{-b\pm \sqrt{b^2-4ac}}{2a}\Downarrow\\ x&=\frac{-(-6)\pm \sqrt{(-6)^2-4\cdot 3\cdot 1}}{2\cdot 3}\Downarrow\\ x&=\frac{6\pm \sqrt{24}}{6}\Downarrow\\ x=0.18&\vee x=1.82 \end{align*}$

x-værdier indsættes i f:

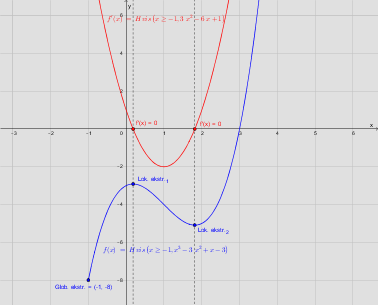
$\begin{align*} f(0.18)&=y_1=(0.18)^3-3\cdot (0.18)^2+0.18-3\Downarrow\\ &=-2.91\Downarrow\\ Lok.\;ekstr._1&=(0.18,-2.91)\\\\ f(1.82)&=y_2=(1.82)^3-3\cdot (1.82)^2+1.82-3\Downarrow\\ &=-5.09\\ Lok.\;ekstr._2&=(1.82,-5.09)\\ \end{align*}$

Værdimængde (Vm(f)):

$\begin{align*}Vm(f)&=[-8;\infty] \end{align*}$

Vedhæftet fil:C_M_019 - Ekstrema og Værdimængde_Johan873.png

Svar #8
18. juli 2018 af Johan873 (Slettet)

Tak for hjælpen! :D

Skriv et svar til: Ekstrema og Værdimængde

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.