Matematik
Krumningens maximum
Hej
Jeg sidder med en opgave men er ikke helt sikker, hvordan jeg skal gøre. Den siger følgende:
Find the point or points on the given curve at which the curvature is a maximum. ,
.
Det jeg tænker er, at man skal benytte formlen for krumningen: , hvor jeg så for det til at se således ud:
. Og efter jeg har reduceret det, får jeg følgende:
.
I den sidste del, hvor jeg er kommet frem til 20, har jeg brugt IDIOTformlen. Er det korrekt, hvad jeg har gjort indtil videre. Hvis ja hvad skal man så derefter? Og hvis ikke, hvad skal man så???
På forhånd tak!
Svar #1
19. september 2018 af Warrio
Jeg kan allerede se, at jeg har tastet noget forkert..... I formlen har jeg indsat 4 istedet for 3, og jeg her ved en fejl tastet 4*sin(t) i nævneren, ved den første udtryk -_- Det må I undskylde, men jeg har den rigtige udregning her:
.
Svar #2
19. september 2018 af swpply (Slettet)
Efter at du har bestemt krumningen som funktion af parameteren t skal du finde maksima for funktion. Dette gør du ved at differentiere dit udtryk for krumningen med hensyn til t, find så den t værdi forhvillken den afledte af krumningen forsvinder. Afgør ved monotoni overvejelser for hvilke af disse t værdier krumningen er maksimum. Punktet hvor krumningen er maksimum udregnes ved brug af x = 5*cos(t) og y = 3*sin(t).
Svar #4
19. september 2018 af Warrio
Mange tak for svaret!
bare en lille ting til. Jeg får nemlig tre værdier.... og
og 0. Hvilken værdi skal jeg bruge for at kunne beregne punktet ud.
Svar #5
19. september 2018 af Warrio
Og ifølge bogen, hvis jeg bruger værdien får jeg punktet hvor krumningen er minimum? Har jeg gjort noget forkert?
Svar #6
19. september 2018 af guuoo2
Kurven er lukket og glat (lokalt), så maksimum findes i et stationært punkt. Dvs. dets værdi er
Flere af mulighederne kan dog godt være lige store.
Svar #7
19. september 2018 af swpply (Slettet)
Du bør finde fire værider, gundet at kurven (x(t),y(t)) = (5*cos(t),3*sin(t)) er en ellipse med halv storakse 5 og halv lilleakse 3. De fire t-værdier er (0, π/2, π, 3π/2).
Du skal afgøre hvilke af de fire t-værdier der er maksimum ved enten at analysere monotoni forholdet for k(t) eller ved at afgøre for hvilke af t-værdierne (0, π/2, π, 3π/2) at k''(t) > 0 (bemærk dette er den anden afledte af krumningen).
-- Dette er ikke anderledes end at besteme maksimum for en hvilken som helst anden funktion f. Det er jeg sikker på at du har gjort et utal ag gange i undervisningen fra gymnasiet.
Svar #8
19. september 2018 af swpply (Slettet)
#6 det er selvfølgelig korrekt og også langt den nemmeste måde at afgøre dette på :-)
Svar #9
19. september 2018 af Warrio
Jo det har jeg, men ikke hvor man skal bestemme punktet .... Kun i hvilken interval funktionen er voksende eller aftagende.
Jeg bruger en cas-værktøj (maple), for at bestemme k'(t)=0, for at bestemme værdierne for t.... men jeg får nemlig kun de 3 værdi som skrevet i #4.
Jeg tænkte derfor, om det var anderledes på en måde, eller så er det bare mig som stadig gøre det forkert?
Svar #11
19. september 2018 af swpply (Slettet)
#9Jeg tænkte derfor, om det var anderledes på en måde, eller så er det bare mig som stadig gøre det forkert?
Du gør det principielt ikke forket, jeg tror bare at du kun kigger efter løsninger for -π/2 < t < π/2 istedet for det fulde interval -π/2 ≤ t < π/2.
Ja der er en anden måde, lidt flabet heder den kuglepen og papir ;-)
Du har at
Hvorfor at hvis og kun hvis
eller
, eftersom
for alle
.
Svar #12
20. september 2018 af Warrio
hvordan har du differentieret den? når det er med parpir og plyant XD
Svar #13
20. september 2018 af swpply (Slettet)
Begynd med at observer at du kan skrive kumningen
som følgende:
Hvorfor at den afledte nemt udregnes ved brug af de sædvanlige regneregler for differentation af en potensfunktion og differentation af en sammensat funktion:
Hvorfor at
Svar #14
20. september 2018 af swpply (Slettet)
I forlængelse af #13 kan du ved brug af #6 nemt indse at krumningen antager maxima når
Og ved at bruge at
kan du slutte at krumningen antager maxima i punkterne og
.
Svar #15
20. september 2018 af swpply (Slettet)
Svar #16
20. september 2018 af swpply (Slettet)
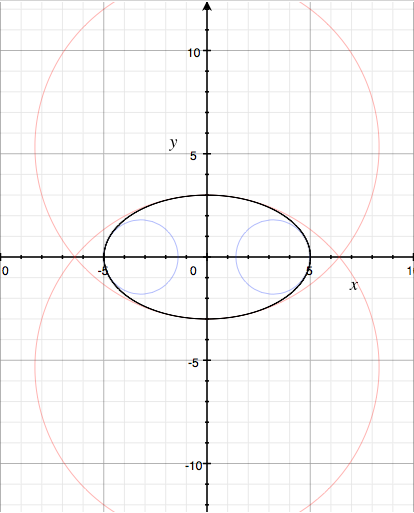
Ovenstående er et billed af kurven (x(t), y(t)) = (5*cos(t), 3*sin(t)) set som den sorte ellipse.
Det to blå cirkler svare til krumningscirklerne hørende til maxima for krumningen, tilsvarende er de to røde cirkler krumningscirklerne hørende til minima for krumningen.
Skriv et svar til: Krumningens maximum
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.

