Matematik

Trigonometriske funktioner

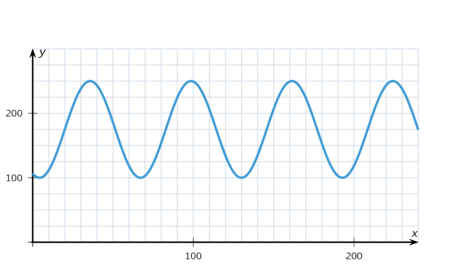
22. oktober 2018 af georgyzhukov666 - Niveau: B-niveau

Hvordan bestemmer man forskriften for en harmonisk svingning, ud for et billede? Har ingen ide hvor jeg skal starte...

Vedhæftet fil: funktion.png

Brugbart svar (0)

Svar #1
22. oktober 2018 af StoreNord

Så skulle du måske spørge din lærer, hvornår han vil gennemgå emnet.
Og så høre efter.

Brugbart svar (0)

Svar #2
22. oktober 2018 af Maksmankovskylenin1917

Slettet

Brugbart svar (0)

Svar #3
22. oktober 2018 af StoreNord

Så er det jo godt han har dig til at hjælpe ham med en opgave om et emne, som han først lærer om senere på ugen. I dag var 1. dag efter ferien, så det er ikke utænkeligt, at det forholder sig sådan.

Svar #4
22. oktober 2018 af georgyzhukov666

Situationen er den, at vi har fået afleveringen for til i dag her kl 20, men at jeg først er kommet sent i gang. Vi har ikke haft om netop dette emne før, men vi er blevet udstyret med en i min mening uforståelig bog. Jeg håbede at jeg ville kunne få hjælp her, ligesom jeg så ofte ser andre få hjælp, men ser ud til at jeg tog fejl.

Brugbart svar (0)

Svar #5
22. oktober 2018 af Maksmankovskylenin1917

Slettet

Brugbart svar (0)

Svar #6
22. oktober 2018 af swpply (Slettet)

Brugbart svar (0)

Svar #7
22. oktober 2018 af swpply (Slettet)

Den harmoniske svigning kan beskrives ved funktionen

$f(x) = A\cos(\omega t-\varphi)$

hvor tallet $A$ betegnes amplitude, tallet $\omega$ betegnes vinkelfrekvensen og $\varphi$ benævnes fasen.

Eftersom at cosinus funktion kun kan antage værider imellem -1 og 1, så gælder der selvsagt at 2 gange amplituden er bestemt ved forskelen imellem kurvens lokale maksimum og kurvens lokale minimum. Hvorfor at

$2A = 250-100 \quad\Leftrightarrow\quad A = 75$

Vinkelfrekvensen $\omega$ er relateret til frekvensen $f$ ved at $\omega = 2\pi f$ . Brug nu at der om perioden $T$ og frekvensen for en harmoniske svigning gælder at de er omvendt proportionale. Hvorfor at

$\omega = \frac{2\pi}{T}$

Perioden kan eks. aflæse af grafen ved at finde afstanden imellem to på hinanden bølge toppe. Du har dermed at $T = 100 - 35 = 65$ , hvorfor at

$\omega = \frac{2\pi}{65}$

Fasen bestemes ved at $\cos(0) = 1$ , hvorfor at (afstanden til første bølge top)

$\varphi = 35$

Dermed har du at

$f(x) =75\cdot\cos\bigg(\frac{2\pi}{65}\cdot t-35\bigg)$
______________________________________________________________________________________

PS. Maksmankovskylenin1917's stødende og uanstændige sprogbrug er anmeldt til moderator. Eftersom at en sådan tone er i uoverensstemmelse med forumets sprogbrug og politik herom. Se punkt to under generelle råd (link).

Brugbart svar (0)

Svar #8
23. oktober 2018 af ringstedLC

En harmonisk svingning er en sinuskurve, altså grafen for funktionen sinus.

1. Den er periodisk (dvs. gentages). Perioden i enhedscirklen er 2π.

2. Den har en amplitude (udsving, fx af en guitarstreng).

3. Den kan som her være faseforskudt (Φ), altså forskudt i x-retningen (en "standard" sinuskurve går igennem (0,0)).

4. Den kan som her være forskudt (C) i y-retningen.

Forskrift:

$\begin{align*} f(x) &= Ampl\cdot \sin\left (\frac{2\pi}{p} x+\phi \right )+C\\ \end{align*}$

Perioden findes ved at tælle tern mellem bølgetoppe. Ligeså for amplituden.

$\begin{align*} f(x) &= 75\cdot \sin\left (\frac{2\pi}{63} x+1.98 \right )+175\\ \end{align*}$

Vedhæftet fil:B_M_052 - Harm. svingning_georgyzhukov666.png

Brugbart svar (0)

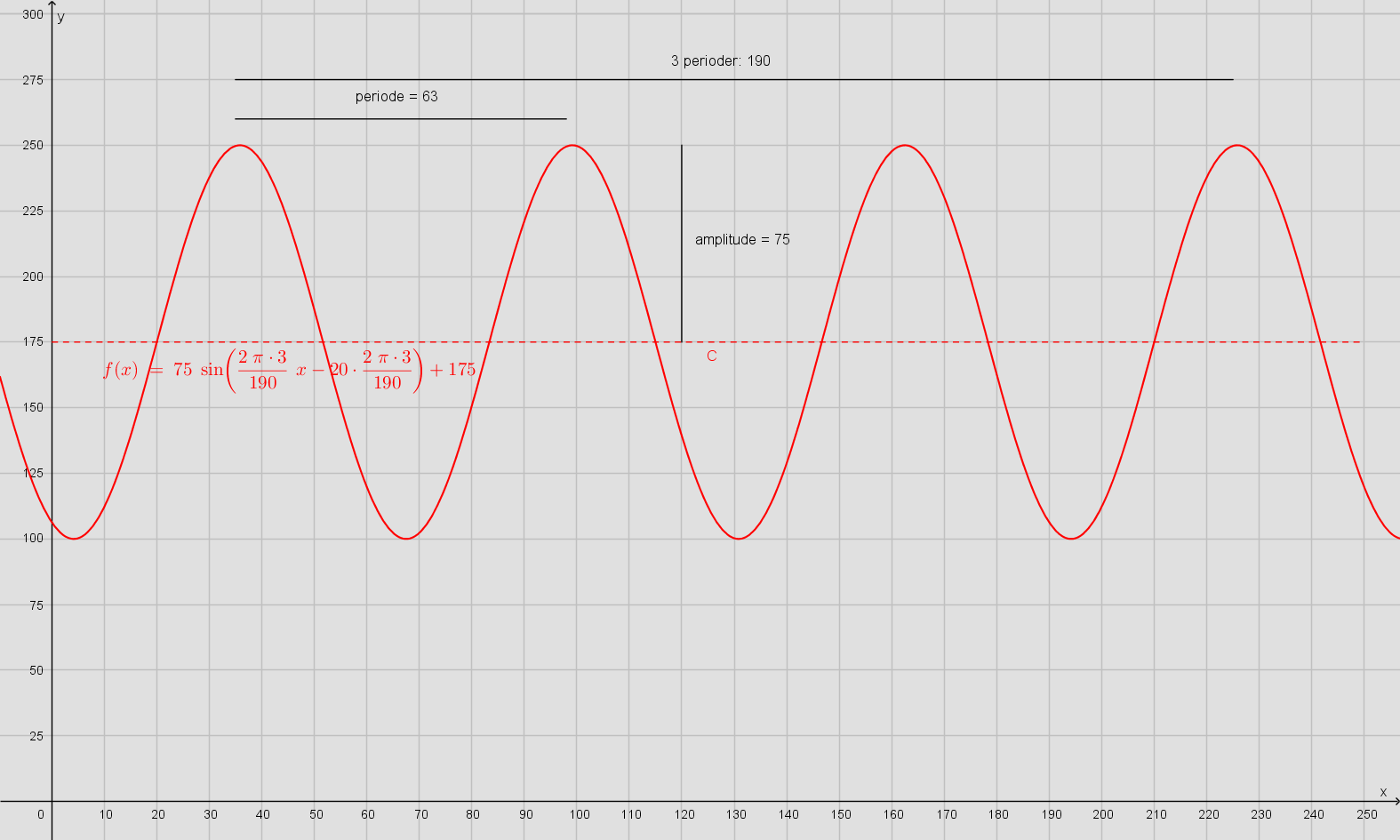
Svar #9
27. oktober 2018 af ringstedLC

Bemærk: Funktionerne i #7 og #8 bliver forskellige af flg. grunde:

1. #7 tager udgangspunkt i cosinus. Det giver en anden faseforskydning, da fasen mellem sinus og cosinus er π/2. Det er ikke forkert, men man kan indvende, at sinus blev "opfundet" før cosinus. Uden sinus, ingen co-sinus.

2. I #8 aflæses og beregnes perioden over det størst mulige interval. Det giver den største aflæsnings-nøjagtighed.

3. #7 omtaler ikke forskydningen i y-retningen. Det er en fejl.

Endelig benævnes funktionen f(x) i #7, hvorefter variablen benævnes t. Det er en fejl.

Skriv et svar til: Trigonometriske funktioner

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.