Matematik

Integralregning spg

18. februar 2019 af WhatTheFu - Niveau: A-niveau

Hej alle.

Jeg sidder med en opgave jeg ikke lige kan finde ud af - jeg har forsøgt at sætte f(x)=g(x) hvor jeg får tallene -4,31 samt 4,31 som x værdier. Skal jeg så sætte a som værende -4,31 og b som 4,31, men hvad med informationen om x = -3?

Og hvordan bestemmer jeg rumfanget når legemet omdrejes 360 grader?

Vedhæftet fil: opg 1 integral.PNG

Brugbart svar (1)

Svar #1
18. februar 2019 af PeterValberg

Jeg indsætter lige dit billede, det gør det lidt nemmere at hjælpe dig

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (1)

Svar #2
18. februar 2019 af PeterValberg

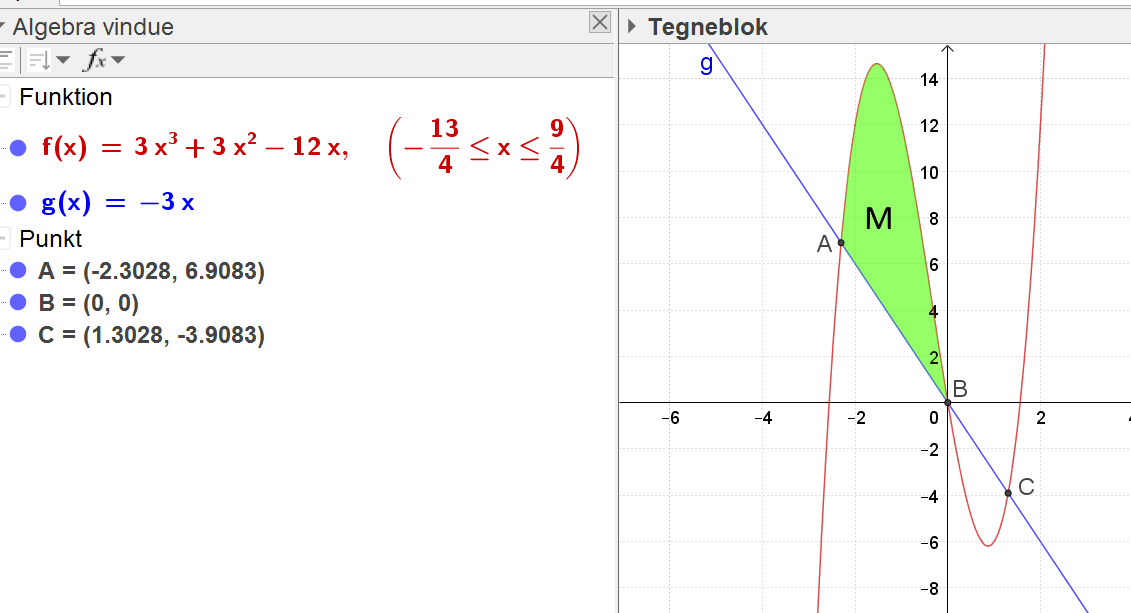
Du bestemmer ganske rigtigt x-koordinaterne til skæringspunkterne mellem f og linjen m
ved at sætte deres forskrifter lig med hinanden.

- - -

mvh.

Peter Valberg
(YouTube)

Vedhæftet fil:Unavngivet.png

Brugbart svar (1)

Svar #3
18. februar 2019 af PeterValberg

Hvis linjen m beskrives med forskriften g(x) = -3x
kan arealet af punktmængden M bestemmes som:

$A_M=\int_{x_A}^{x_B}{(f(x)-g(x))dx}$

hvor x_A og x_B er x-koordinaterne for skæringspunkterne A og B (jf. tegning i #2)

- - -

mvh.

Peter Valberg
(YouTube)

Svar #4
18. februar 2019 af WhatTheFu

#2

Du bestemmer ganske rigtigt x-koordinaterne til skæringspunkterne mellem f og linjen m
ved at sætte deres forskrifter lig med hinanden.

Mange tak! Jeg har lige grublet og grublet, og så fundet ud af jeg har vedhæftet den forkerte opgave!

Vedhæftet fil:opg 3 inttegral.PNG

Brugbart svar (0)

Svar #5
18. februar 2019 af mathon

$\small \small \small \small \begin{array}{rcrclcl} f(x)&=&g(x)=-3x\\\\ 3x^3+3x^2-12x&=&-3x\\\\ 3x^3+3x^2-9x&=&0&\textup{s\ae t 3x uden for parentes}\\\\ 3x\left ( x^2+x-3 \right )&=&0\\\\ x&=&\left\{\begin{matrix} \frac{-1-\sqrt{13}}{2}\\0 \\ \frac{-1+\sqrt{13}}{2} \end{matrix}\right. \end{array}$

Brugbart svar (0)

Svar #6
18. februar 2019 af AMelev

#0 Dine løsninger til f(x) = g(x) er forkerte jf. #2. Hvordan har du fået dem?
Det er altid en god idé at tegne graferne, så kan du tjekke, og det er lettere at se, hvilket område, der er tale om.

Rumfanget af det omdrejningslgeme, der fås ved at dreje punktmængden M 360º om 1.aksen kan beregnes ved at bestemme rumfanget af legemet, der fås ved at dreje punktmængden under f-grafen mellem x_A og x_B.
Derfra trækker du rumfanget af omdrejningslegemet af området under g(x) mellem x_A og x_B.

Skriv et svar til: Integralregning spg

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.