Log

4log(x)+8Log(y)  = log(x⁴)+log(y⁸) = 5  endvidere skal du bruge at log(a) = 5 <=> a=10⁵

#1

4log(x)+8Log(y)  = log(x⁴)+log(y⁸) = 5  endvidere skal du bruge at log(a) = 5 <=> a=10⁵

Kunne du måske forklare det yderligere? For jeg forstår det stadig ikke

Benyt to nye variable X = logx og Y=logy. Så får du to ligninger med to ubekendte. Dem løser du på sædvanlig måde. Derefter tager regner du x og y ud.

#3

Benyt to nye variable X = logx og Y=logy. Så får du to ligninger med to ubekendte. Dem løser du på sædvanlig måde. Derefter tager regner du x og y ud.

Så jeg skal regne det som 2 ligner med 2 ubekendte? Så det ville sige 4x og 8y=11 ? Men for at bruge den metode skal jeg vel også bruge den nederste ligning så det bliver 6logx-6logy=-3

logx³ = 3logx, tilsvarende med de andre led. Når du har skrevet den alle om, har du en simpel ligning med logx som ubekendt. Den løser du og finder så x bagefter.

ikke 4x og 8y, men 4X+8Y=11 og tilsvarende i den anden ligning. x og X er ikke det samme.

#6

ikke 4x og 8y, men 4X+8Y=11 og tilsvarende i den anden ligning. x og X er ikke det samme.

Okay, men det ville sige at jeg skal bruge begge ligninger for at kunne løse opgaven?

Logaritmereglerne
L0: Log(10^x) = 10^Log(x) = x            "Log og 10^ ophæver hinanden"
L1: Log(x·y) = Log(x) + Log(y)
L2: Log(x/y) =  Log(x) - Log(y)
L3: Log(xⁿ) = n·Log(x)

4·logx+8·logy=5 (L3) ⇔ Log(x⁴) + Log(y⁸) = 5 (L1) ⇔ Log(x⁴·y⁸) = 5 (L0) ⇔ x⁴·y⁸ = 10⁵

6·logx-6·logy=-3 som ovenfor, men med L2 i stedet for L1

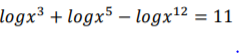 L1, L2, potensregler, L0

#7 Ja, du skal løse dem helt som du ellers ville og så til sidst tage antilogaritmen.

#8

Logaritmereglerne
L0: Log(10^x) = 10^Log(x) = x            "Log og 10^ ophæver hinanden"
L1: Log(x·y) = Log(x) + Log(y)
L2: Log(x/y) =  Log(x) - Log(y)
L3: Log(xⁿ) = n·Log(x)

4·logx+8·logy=5 (L3) ⇔ Log(x⁴) + Log(y⁸) = 5 (L1) ⇔ Log(x⁴·y⁸) = 5 (L0) ⇔ x⁴·y⁸ = 10⁵

6·logx-6·logy=-3 som ovenfor, men med L2 i stedet for L1

 L1, L2, potensregler, L0

Så i den første er svaret så x^4*y8=10^5?

Jeg formoder, at opgaven går ud på at finde x og y. Hvis det er tilfældet, er x⁴y⁸=10⁵ ikke svaret.Det er en omskrivning af den første ligning.

#11

Jeg formoder, at opgaven går ud på at finde x og y. Hvis det er tilfældet, er x⁴y⁸=10⁵ ikke svaret.Det er en omskrivning af den første ligning.

Men hvordan skal jeg så løse den? Da jeg prøvede med to ligninger med to ubekendte fik jeg 39=42y hvilket ikke giver mening da resultat ville være et kommatal

Hvis du dividerer 39=42y med 42 på begge sider af lighedstegnet, får du et kommatal.

Jeg kan ikke se, hvordan du er kommet frem til den ligning, og du mangle at finde x.

#13

Jeg brugte substitutionsmetoden

Jeg får et ander tal. Jeg får 72logy=42.

Det er både ved substitution og ved lige store koefficienter. Bemærk, at det er logy, ikke y, jeg har fundet.

#15

Jeg får et ander tal. Jeg får 72logy=42.

Det er både ved substitution og ved lige store koefficienter. Bemærk, at det er logy, ikke y, jeg har fundet.

Men hvordan fjerner man log? Bliver det bare 72=42₁₀ ?

Nej, man starter med at dividere ligningen igennem med 72. Så får man logy = 42/72 = 0,583333. Derefter tager man antilogaritmen til tallet. På lommeregner hedder det sikkert INV LOG.

Når du har det, skal du også finde x.

I #0 skriver du, at du har 3 opgaver.
Hvis det er rigitgt, kan de to første kun reduceres ikke løses, da der er to ubekendte x og y.

Generelt er det en god ide at tage et billede af opgaveformuleringen, så man ikke kommer til at gengive en eventuel misforståelse.