Matematik

vektorer

13. april 2019 af Teriperry - Niveau: B-niveau

jeg har stået og prøvet at løse denne opgave, men kan simpelthen ikke komme frem til det rigtige facit. jeg ved ikke hvad jeg gør forkert så det ville være virkelig hjælpsomt med noget hjælp:)!

i et koordinatsystem er der givet et punkt A(-15,29) og en linje m med parameterfremstillingen m: $m:(x,y) = (8,15)+t(5,2)$

for ethvert t bestemmer parameterfremstillingen et punkt P på linjen.

A) bestem koordinatsættet til vektor AP udtrykt ved t

B) bestem t, så vektor AP $\perp$ (5,2), og bestem koordinatsættet til P

Brugbart svar (0)

Svar #1
14. april 2019 af jnl123

A) Træk A fra P som funktion af t for at bestemme AP udtrykt ved t:

AP(t) = P(t) - A = (8,15) + t(5,2) - (-15,29) = ?

B) Opstil en ligning og isoler t. Brug resultatet fra A) og at skalarproduktet mellem AP og vektoren (5,2) er lig 0 hvis de er vinkelrette.

Svar #2
14. april 2019 af Teriperry

#1
A) Træk A fra P som funktion af t for at bestemme AP udtrykt ved t:

AP(t) = P(t) - A = (8,15) + t(5,2) - (-15,29) = ?

B) Opstil en ligning og isoler t. Brug resultatet fra A) og at skalarproduktet mellem AP og vektoren (5,2) er lig 0 hvis de er vinkelrette.

okay tusind tak, men forsåtr ikke lige helt hvordan jeg laver b altså det gvier ingen mening når jeg prøver at regne det ud med skalarprodukts formlen

Brugbart svar (0)

Svar #3
14. april 2019 af mathon

$\small \overrightarrow{AP}=\begin{pmatrix} 23+5t\\-14+2t \end{pmatrix}$

$\small \begin{pmatrix} 23+5t\\-14+2t \end{pmatrix}\cdot \begin{pmatrix} 5\\2 \end{pmatrix}=0$

$\small (23+5t)\cdot 5+( -14+2t)\cdot 2=0$

$\small 115+25t-28+4t=0$

$\small 29t=-87$

$\small t=-\tfrac{87}{29}$

$\small t=-3$

$\small P=\left ( 8+(-3)\cdot 5\, ;15+(-3) \cdot 2\right )=(-7\, ;9)$

Brugbart svar (0)

Svar #4
14. april 2019 af AMelev

#0 P(8 + 5t,15 + 2t)
Ad A) Du bør i besvarelsen skelne mellem punkter og vektorer, men da stedvektorerne har samme koordinatsæt som punkterne, bliver resultatet det samme som i #1. $\overrightarrow{AP}=\overrightarrow{OP}-\overrightarrow{OA}$ .

Ad B) Da (5,2) er retningsvektor for linjen, kan P bestemmes som skæringspunktet mellem linjen og dens vinkelrette gennem A.

Vedhæftet fil:Billede1.jpg

Brugbart svar (0)

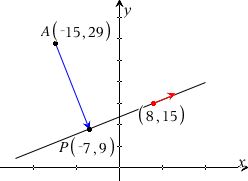
Svar #5
14. april 2019 af ringstedLC

Udtrykket fra A)

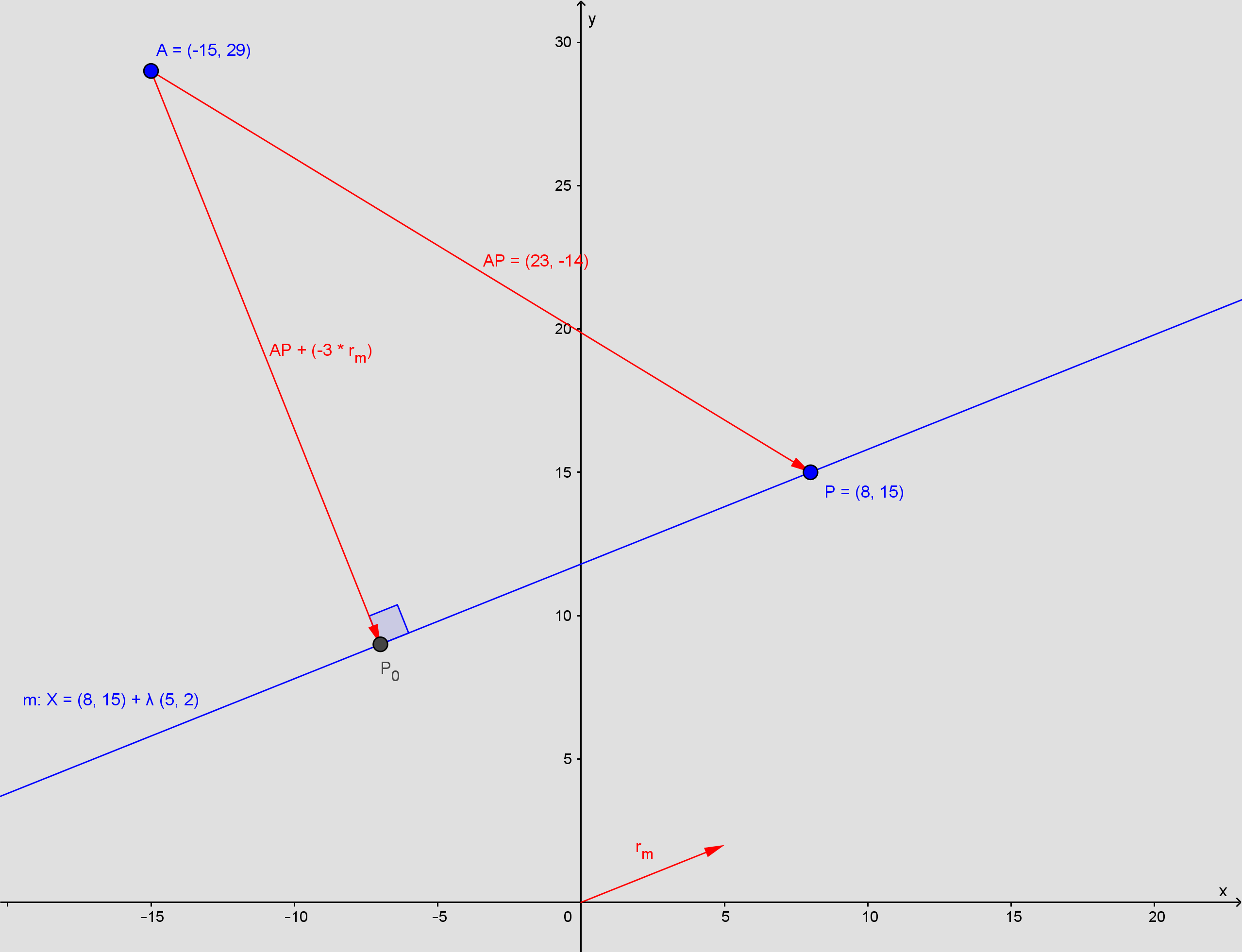
$\begin{align*} \binom{8-(-15)+5t}{15-29+2t}\cdot \binom{5t}{2t} &= 0\;,\;t\neq0 \\ \binom{23+5t}{-14+2t}\cdot \binom{5t}{2t} &= 0 \\ (23+5t)\cdot 5t+(-14+2t)\cdot 2t &= 0 \\ 29t^2+87t &= 0 \\ t &= -3 \end{align*}$

Vedhæftet fil:B_M_079 - Skalarprodukt_Teriperry.png

Skriv et svar til: vektorer

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.