Matematik

Funktionsforskrift

20. maj 2019 af johanne1212 - Niveau: 10. klasse

Jeg har fået en matematikopgave, der siger at jeg skal finde en funktionsforskrift der viser dette:
- Indbyggertal på 1.000.000 det første år,
- Der dør flere end der bliver født, hvilket resulterer i et 5% fald i befolkningstallet årligt.
- Der flytter hvert år 70.000 mennesker til.
- 10.000 flytter væk årligt.

Er der nogen der kan hjælpe mig? Tak!!

Brugbart svar (0)

Svar #1
20. maj 2019 af peter lind

y = (1000000+(70000-10000)x)*0,95^xHvor x er antal år

Brugbart svar (0)

Svar #2
20. maj 2019 af oppenede

Betingelserne kan udtrykkes ved differentialligningen:
$\\y'(t)=\ln(0.95)y(t)+60000 \\y(0)=1000000$

som du kan løse med panserformlen, hvilket giver:
$y(t)=1000000\cdot 0.95^t+\frac{60000}{-\ln(0.95)}(1-0.95^t)$

Bemærk #1 er helt hen i vejret: Hvis man indsætter f.eks x=100 giver formlen 41444 og året efter (x = 101) giver det 39709, så mindst 20000 af de 60000 nytilflyttede dør på et år, hvilket ikke stemmer overens med de angivne betingelser.

Brugbart svar (0)

Svar #3
20. maj 2019 af peter lind

#2 : Det giver ialt et fald på 1735 personer. en del overlevende fra forrige år er også døde . Hvordan får du at over 20000 af de nytilkommende dør. Der dør faktisk 60000*0.05 = 3000 af dem der kom forrige år

Brugbart svar (0)

Svar #4
21. maj 2019 af AMelev

Ad #2 Til gengæld er differentialligninger nok "en anelse" over 10. klasses niveau.
Desuden kan jeg ikke helt gennemskue differentialligningen

Der er lidt usikkerhed i formuleringen. Har du kopieret hele opgaveformuleringgen over? Hvis ikke, så læg lige et billede af den op.

Hvis de 5% nedgang også ivolverer immigrationen, så ser jeg det sådan (men jeg kan tage fejl - det er før sket).

Jeg sætter yn til at være indbyggertallet ved starten af det n'te år, altså y0 = 1000000
Netto-immigrationen pr. år er b = 60000
Den procentvise årlige nettotilvækst er r = -5% =-0.05. Netto-"overlevelsen" er så a = 1 + r = 0.95

Så får jeg y1 = (y0 + b)·a = a·y0 + a·b
y2 beregnes tilsvarende: y2 = (y1 + b)·a = (a·y0 + a·b + b)·a = y0·a² + a²·b + a·b
y3= (y2 + b)·a = (y0·a² + a²·b + a·b + b)·a = y0·a³+ a³·b + a²·b + a·b
y4= (y3 + b)·a = (y0·a³ + a³·b + a²·b + a· b)·a = y0·a⁴+ a⁴·b+a³·b +a²·b + a·b osv.

yn = y0·aⁿ + (aⁿ·b + a^n-1·b +.... + a²·b + a·b) = y0·aⁿ + a·(a^n-1·b + a^n-2·b +.... + a·b + b)

Hvis I har arbejdet med annuitetsopsparing, kan det med fedt fremhævede betragtes som samme problemstilling, bortset fra at der er negativ procentvis tilvækst (rente).
Du kan så benytte fomlen $An = b\frac{(1+r)^n-1}{r}$ til at beregne "annuitetssaldoen".

Dermed får du $yn= y0\cdot a^n+a\cdot \mathbf{60000\cdot \frac{0.95^n-1}{-0.05}}=$ $1000000\cdot 0.95^n+0.95\cdot 60000\cdot \frac{0.95^n-1}{-0.05}$
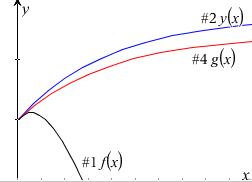
eller hvis du "udvider" til ikke-hele tal $g(x)= 1000000\cdot 0.95^x+0.95\cdot 60000\cdot \frac{0.95^x-1}{-0.05}$ .

Som det fremgår af graferne nedenfor, er vi ikke (helt) enige om modellen.
y(t) i #2 har nogenlunde samme forløb som g(x), men vokser lidt hurtigere. Jeg kan ikke helt gennemskue differentialligningen, så jeg kan ikke sige hvorfor.
g(x) giver imidlertid et helt andet billede af udviklingen end funktionen f(x) i #1, hvilket skyldes, at der i f(x) regnes med, at det procentvise fald beregnes for alle immigranterne i alle x år, men det skal jo først gælde, efter de er kommet til landet.

Denne opgave er da lidt af en barsker på 10. klasses niveau, også selv om I har haft beviset for formlen for opsparingsannuitet eller har arbejdet med sum af kvotientrække i anden sammenhæng.

Vedhæftet fil:Billede2.jpg

Skriv et svar til: Funktionsforskrift

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.