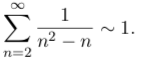Matematik

tilde?

28. maj 2019 af sajana - Niveau: Universitet/Videregående

hej

er der nogen der kan hjælpe mig med denne her opgave?

Vedhæftet fil: Skærmbillede 2019-05-28 kl. 09.31.19.png

Brugbart svar (1)

Svar #1
28. maj 2019 af oppenede

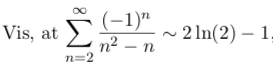
Betragt
$\sum_{n=2}^{\infty }\frac{x^n}{n^2-n}$
og differentier den ledvist:
$\sum_{n=2}^{\infty }\frac{x^{n-1}}{n-1}=\sum_{n=1}^{\infty }\frac{x^{n}}{n}= -{\ln(1-x)}$

Differentation ændrer ikke konvergensradius, så begge summer konvergerer når -1 < x < 1, og begge konvergerer også i ved x = -1, da de er alternerende og monotont aftagende mod 0.

Integrer tilbage:
$x+(1-x)\ln(1-x)+k$
Ved x = 0 giver den oprindelige sum 0, så k = 0. Dermed fås for x = -1:
$-1+(1-(-1))\ln(1-(-1))=2\ln(2)-1=\sum_{n=2}^{\infty }\frac{(-1)^n}{n^2-n}$

Jeg ved ikke hvorfor der står tilde. Slå op i pensum og se hvordan det er defineret.

Svar #2
28. maj 2019 af sajana

hvad betyder det der tilde tegn betyder det at den er lig med eller at den nærmer sig?

hvorfor vælger du x=0 eller x=-1?

Brugbart svar (1)

Svar #3
28. maj 2019 af oppenede

x = 0 gør summen triviel hvormed k kan bestemmes. x = -1 svarer til den sum der skal bestemmes.

Svar #4
28. maj 2019 af sajana

har lige sidste spørgsmål: hvordan ved du at summen af x^n/n =-ln(1-x)?

Svar #5
28. maj 2019 af sajana

hvordan kan jeg også vise det for det her. Hvis jeg gør på samme måde så vil jeg få:

summen af 1/n men for n=1 men hvordan fortsætter jeg så

Vedhæftet fil:Skærmbillede 2019-05-28 kl. 19.04.34.png

Brugbart svar (0)

Svar #6
28. maj 2019 af oppenede

#5:

$\\\sum_{n=2}^\infty\frac{1}{n^2-n} =\lim_{m\to\infty} \sum_{n=2}^m\frac{1}{n^2-n} = \lim_{m\to\infty} \sum_{n=2}^m\left(\frac{1}{n-1}-\frac{1}{n}\right) = \\\text{ }\hspace{0.2cm}{\lim_{m\to\infty} \left(\sum_{n=2}^m\frac{1}{n-1}-\sum_{n=2}^m\frac{1}{n}\right) = \lim_{m\to\infty} \left(\sum_{n=1}^{m-1}\frac{1}{n}-\sum_{n=2}^m\frac{1}{n}\right) = \lim_{m\to\infty} \left(\frac{1}{1}-\frac{1}{m}\right) =1}$

#4: Bestem den n'te afledede af -ln(1-x) ved induktion.

Skriv et svar til: tilde?

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.