Fysik

Beregning af vinkelacceleration for en massiv skive

23. juli 2019 af naji0044 - Niveau: Universitet/Videregående

Dav alle

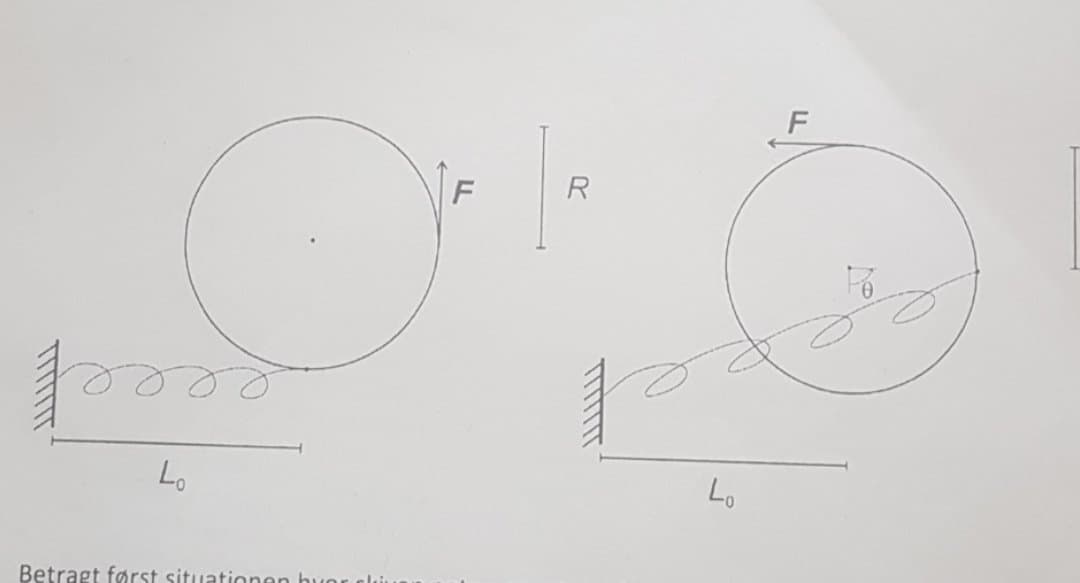
Står lidt i bar bund med denne opgave, som består af en massiv skive. Den er forbundet med en fjeder som i kan se på billedet som viser før og efter situationen, når den påvirkes med en kraft F. Vi ser bort fra friktion og skiven centrum kan frit rotere i den fast lodrette akse.

Massen=10 kg

r=0.735m

L_0=2r

F=233 N

b) Bestem vinkelaccelerationen af skiven ved vinklerne 0* og 90*

Det jeg har gjort er at bestemme vinkelacceleationen udfra formlen:
a=I / t (torque)
hvor I for en massiv skive er : 1/2*m*r^2
og Torque=r*F*Sin(v)
så får jeg at a=0.735m*233N/1/2*10kg*(0.735m)^2=63.4 s^-1

er ikke helt klar over om det er vinklen til v=0 eller 90 jeg benytter, ville meget gerne have en lidt skarpere forståelse indenfor dette :)

Vedhæftet fil: Massiv skive.jpg

Brugbart svar (0)

Svar #1
23. juli 2019 af Soeffi

Brugbart svar (1)

Svar #2
25. juli 2019 af Sveppalyf

α = τ / I

I situationen til venstre virker der kun kraftmomentet fra F idet fjederen ikke er strukket ( jeg antager at L₀ er den ustrakte længde?). Da F virker vinkelret på radius, er kraftmomentet bare τ = F * R. Så vi har

α = F*R / (½*m*R²) = 2F/(mR)

I situationen til højre er fjederen nu strukket og bidrager derfor med et kraftmoment.

Fjederens nye længde kan findes med Pythagoras:

L =√( R² + (L₀ + R)² ) <=>

L = √( R² + (3R)² ) <=>

L = √10 *R

Fjederkraften kan vi så finde med Hookes lov.

F_fjeder = k * ΔL <=>

F_fjeder = k * (L - L_o) <=>

F_fjeder = k * (√10*R - 2R) <=>

F_fjeder = (√10 - 2) *k * R

Vinklen v på tegningen kan vi finde som

tan(v) = 3R/R <=>

v = Arctan(3) ≈ 71,6^o

For at finde kraftmomentet fra fjederkraften skal vi projicere F_fjeder ned vinkelret på radius.

F_{fjeder, proj.} = F_fjeder * cos(v)

og så bliver kraftmomentet fra fjederen

τ_fjeder = F_fjeder * cos(v) * R

Dette kraftmoment virker modsat kraftmomentet fra F, så det resulterende kraftmoment bliver

τ_res = F*R - F_fjeder * cos(v) * R <=>

τ_res = F*R - (√10 - 2) *k * cos(v) * R²

Vinkelaccelerationen bliver så

α = ( F*R - (√10 - 2) *k * cos(v) * R² ) / (½mR²)

Vi kan forkorte med R og flytte ½ op i tælleren.

α = 2( F - (√10 - 2) *k * cos(v) * R ) / (mR)

Brugbart svar (1)

Svar #3
25. juli 2019 af ringstedLC

#0: Du sjusker med dine formler. Uden fjeder:

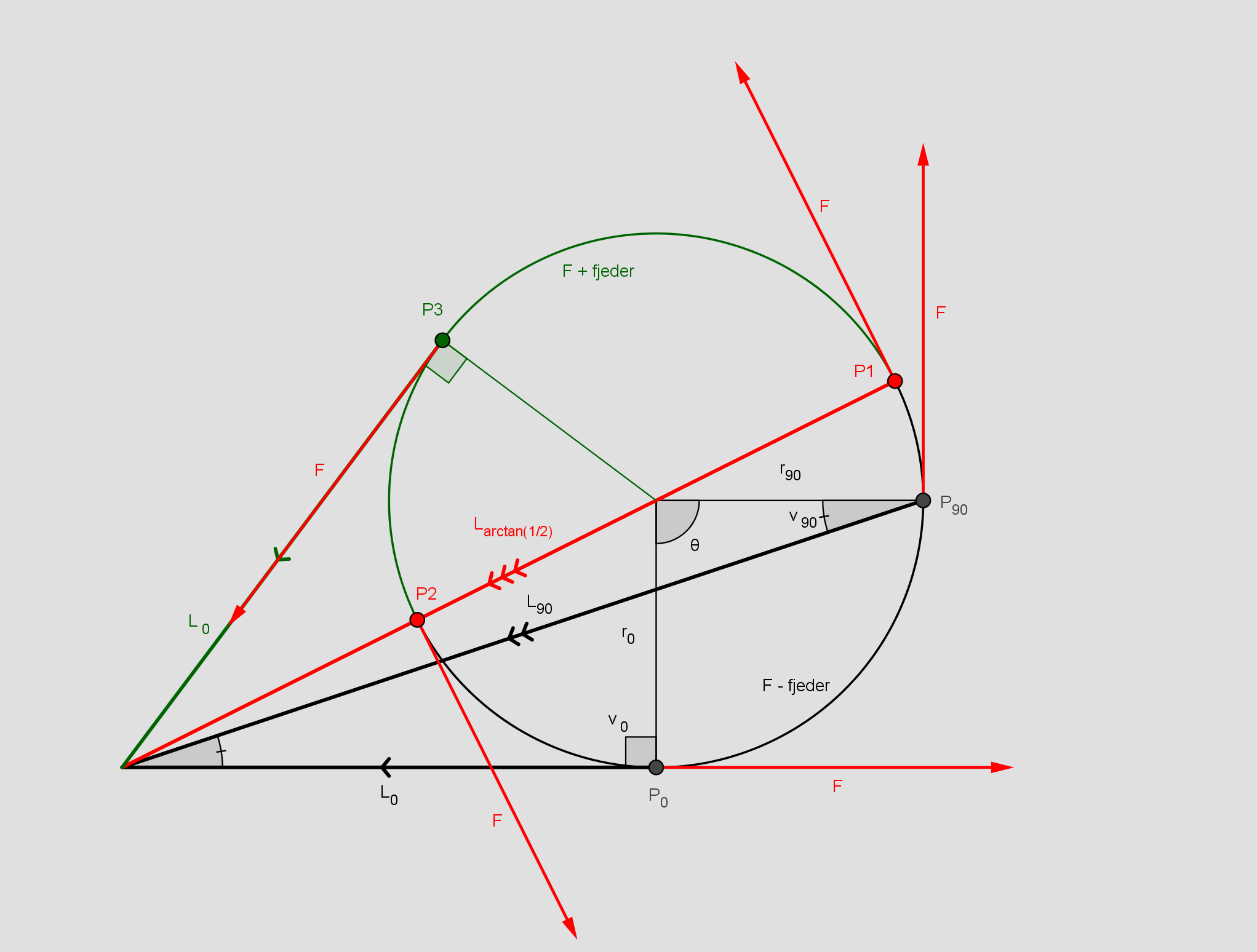
$\begin{align*} \text{ikke}:\alpha_{\Theta} &= {\color{Red} \frac{I}{\tau}} \\ \text{men}: \alpha_{\Theta} &= \frac{\tau}{I} \;,\;I=0.5\cdot m\cdot r^2\;,\;\tau=r\cdot F \\ \alpha_{\Theta} &= \frac{0.735\cdot 233}{0.5\cdot 10\cdot 0.735^2} \;\left ( \frac{m\cdot N}{kg\cdot m^2}=\frac{m\cdot kg\cdot m}{kg\cdot m^2\cdot s^2}=\frac{rad}{s^2} \right )=63.4 \text{ rad/sek}^2 \\\text{i meter}: \alpha &=\alpha_{\Theta}\cdot 2\pi r \\ \alpha &=63.4\cdot 2\pi \cdot 0.735\;\left ( \frac{m}{s^2} \right )=293\text{ m/sek}^2 \end{align*}$

Med fjeder: Kraften F og fjederkraften tangerer skivens periferi. I P₀ er de præcist modsat rettede og derfor reduceres drejningsmomentet med hele (sin(90º) fjederkraften:

$\begin{align*} \text{Fjederens f\ae stningspunkt p\aa \;skiven}&:P \\ \text{En vektor fra }P\text{ til den anden f\ae stning}&:\vec{F}_{fjeder}\\ \text{Vinkel mellem }\vec{F}_{fjeder}\text{ og radien i }P: v &= \left\{\begin{matrix}90^{\circ}\;,\;\Theta=0^{\circ}\text{ (venstre figur)}\\ \tan^{-1}\left ( \frac{r}{3r} \right )\;,\;\Theta=90^{\circ}\text{ (h\o jre figur)}\end{matrix}\right. \\ \text{Totalt drejningsmoment}:& \\\tau &= \tau_{F}+\tau_{fjeder} \\ \tau &= r\cdot F+\sin(v)\cdot F_{fjeder}\;,\;F_{fjeder}=-k\cdot L \end{align*}$ $\begin{align*} \alpha &= \frac{\tau}{I} \\ \alpha_0 &= \frac{r\cdot F-\sin(90^{\circ})\cdot k\cdot 2\cdot r}{0.5\cdot m\cdot r^2}\;,\;L_0=2r \\ \alpha_0 &= \frac{F- 2k}{0.5\cdot m\cdot r}\;\;\;(?:k=\text{ ubekendt)} \\ \alpha_{90} &= \frac{r\cdot F-\sin\left( (\tan^{-1}\left(\frac{1}{3}\right)\right)\cdot k\cdot \sqrt{10r^2}}{0.5\cdot m\cdot r^2} \;,\;L_{90}=\sqrt{\left ( L_0+r \right )^2+r^2} \\ \alpha_{90} &= \frac{F-k}{0.5\cdot m\cdot r} \end{align*}$

Vedhæftet fil:V_F_006 - Vinkelacc._naji0044.png

Svar #4
25. juli 2019 af naji0044

Lavede en tastefejl angående formlen for vinkelaccelerationen. Tak for skitserne, kan ihvertfald se tydeligt nu hvordan fjederkraften påvirker skiven. Har lige et spørgsmål til #1 du siger at fjederkraften er modsat rettet med F, når den projiceres på x planen. Er de ikke samme retning altså fjederen og F, efter 1/4 omgang?

Brugbart svar (1)

Svar #5
25. juli 2019 af Sveppalyf

Kraftmomentet fra F forsøger at dreje skiven mod uret. Kraftmomentet fra fjederkraften forsøger at dreje skiven med uret.

Jeg splitter F_fjeder op i en komposant som peger i radiær retning (ind mod skivens centrum) og en komposant som peger i tangential retning (vinkelret på radius, dvs. i situationen til højre er det lodret nedad). Den radiære komposant bidrager ikke til kraftmomentet, så den ser vi bare bort fra.

Brugbart svar (1)

Svar #6
25. juli 2019 af ringstedLC

#4
Har lige et spørgsmål til #1 du siger at fjederkraften er modsat rettet med F, når den projiceres på x planen. Er de ikke samme retning altså fjederen og F, efter 1/4 omgang?

Nej, F er blot vist to vilkårlige steder på omløbet. F virker tangentielt i ethvert punkt på omløbet.
To steder, P1 og P2 er fjederkraften vinkelret på F og derfor ligegyldig. To steder, P₀ og P3 er den parrallel med F. På den sorte cirkelbue (F - fjeder) giver den modløb og på den grønne (F + fjeder) giver den medløb.

Bemærk: Fjederen er her udspændt under hele rotationen, hvilket i praksis er mest sandsynligt, men ikke har betydning for din udregning.

Svar #7
26. juli 2019 af naji0044

Det hele giver ihvertfald mere mening nu, ihvertfald efter 1/4 omgang er fjederen i modsat retning iforhold til F. Jeg takker for begge jeres svar!

Skriv et svar til: Beregning af vinkelacceleration for en massiv skive

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.